Күрделі пайыздар схемасы бойынша қаржылықəрекеттерді дамыту модельдері.
Егер пайыздық ақша B (несиеге берген капиталдан түскентабыс) алғашқы несиеге берген капиталға (ақшаға) A қосылып,келесі кезекте сол барлық толтырылған (A+B) сомадан пайыздықақша есептелінсе, онда қаржылық əрекеттерде күрделі пайыздарсхемасы қолданылады. Кейде осы нұсқаны капитализациялаунемесе реинвестирлеу (алғашқы инвестірленген ақша мөлшерінкөбейту) немесе «пайыздан пайызға» деп аталынады. А н ы қ т а м а. Егер несиелік келісімде жылдықпайыздық үстеме негізінде күрделі пайыздар схемасы бойыншаесептеу қарастырылса, онда t жылдар өткеннен кейін несие берушіқарызгерден C = A( 1 + p)t, (2.18) соманы алады, ал пайыздық ақша мына формула бойыншаесептелінеді B(t) = A( 1 + p)t– A, (2.19) 1. Е с к е р т п е. Несие бүтін бірнеше жылдарға берілген жағдайда,егер t = n, онда (2.17) жəне (2.18) формулалар бірін–бірі қайталайды, яғниекеуімен де есептеу нəтижесі бірдей болады. Сонымен, күрделі пайыздар схемасы бойынша іске қойылғанкапиталдың (ақшаның) мөлшерінің өзгеріс заңдылығынбейнелейтін жалпы математикалық модельді, мынадайгеометриялық прогрессия түрінде жазуға болады: C m = A( 1 + p)m, m = 0, 1, 2, …, n (2.20) Немесе C = A( 1 + p)n = A( 1 +p)t/K = A·kn, (2.21) мұндағы t – келісімшартмерзімініңұзақтығы, күндер; kn – ұлғайтукоэффициенті. Күрделіпайыздартүсінігінкелесіситуацияларменкөрнектеугеболады. Банктіңклиентіжылдық p пайыздықүстемеменқарапайымпайыздарсхемасыбойыншаесептелінетінкелісімбойыншажылбасындадепозиттікшотқа A сомасын 1жылғасалдыделік. (2.4) формулабойыншажылөткенненкейінклиенттіңшотында A( 1 + + p) сомасыпайдаболады, оныклиентшоттантағыдашығарыпаладыда, қайтадансолкелісімжағдайыменбұрынғыдепозиттікшотқаорналастырсын. (Мұндайəрекеттіқаржылықұғымдапайыздықақшасыменбіргеалғашқысома реинвестирленді делінеді, яғниалғашқысалымпайыздықақшағакөбейдінемесеалғашқы инвестицияның;мөлшерінкөбейтсек, осы əрекетіміз реинвестирлендіру депаталады). Осыдан кейінекіншіжылыклиенттіңшотында A( 1 + p)2 сомапайдаболады,үшіншіжылы – A( 1 + p)3 жəне əріқарайжалғасабереді. Сөйтіп, реинвестирлендіру (капитализация) жасаған сайын депозиттегі сома күрделі пайыздар схемасы бойынша геометриялық прогрессия заңдылығымен үстемелене береді. Осыған байланысты, депозит тік шоттан мөлшері бірдей ақшаны,біресе шығарыпалып, одан оған қайтасалып, клиенттің өмірін жəне банктің жұмысын қиындат пау үшін депозиттегі ақшаны үстемелеудік үрделі пайыздар схемасы бойынша есептеу енгізілді. Ескертпе. Егер t = 1 болса, яғниақшақарызға 1 жылғанесиегеалынса, онда қарапайым (2.11) жəнекүрделі (2.18) пайыздарсхемасыбойыншаесептеунəтижелерібірдей, соныменқатар (2.4) формуласыменсəйкескеледі, яғни C=A( 1 +p). Егер несиеге берілген ақшаны қайтаратын мерзім (1 < t <;1) бір жыл данөзгеше болса, онда (2.12) жəне (2.15) формулалармен есептеу нəтижелері əртүрлі болады. Ескертпе. Несиеге берілген ақшаны қайтаратын мерзім(t>;1) біржылдан көпболған жағдайда, мынадай теңсізді корындалынады: A( 1 + p)t >A( 1 + pt), Яғни күрделі пайыздар схемасы бойынша есептесу қарызданушыға пайдалы. Ескертпе. Несиегеберілгенақшанықайтаратынмерзім (t <;1)біржылданкішіболғанжағдайда, мынадайтеңсіздікорындалынады: A( 1 + p)t < A( 1 + pt), яғникүрделіпайыздарсхемасыбойыншаесептесу несиеберушіге пайдалы. Ескертпе. Несиегеақша (t <;1) біржылданазмерзімгеберілгенжағдайда, есептеу, ережесияқты, міндеттітүрдеқарапайымпайыздарсхемасыбойыншажүргізіледі. Несиегеақша (t >;1) біржылданкөпмерзімге берілгенде, үшжағдайболуымүмкін: – есептеуқарапайымпайыздарсхемасыбойынша; – есептеукүрделіпайыздарсхемасыбойынша; – есептеуаралассхемаларбойынша. Несиеге ақша берілген мерзім бүтін санды жыл болмаған жағдайда,есептеу аралас схемалар бойынша келесіқ алыпта жүргізіледі: 1) бүтін санды жыл бойы бастапқы A сома несиені қолданғаны үшін күрделі пайыздар схемасы бойынша оны пайыздық ақшаға ұлғайту есебі жүргізіледі; 2) осы уақытқа дейін жиналған төленбеген соманы қалған жылдың толық емес бөлігі ненесиені қолданғаны үшін қарапайым пайыздар схемасы бойынша пайыздық ақшаға ұлғайту есебі жүргізіледі. Қарапайым жəне күрделі пайыздар схемасы бойынша есептік үстеме негізінде жылдармен өлшенетін мерзімге ссудаберу. Қарызды қайтаратын t мерзім жылдармен өлшенетін жағдайды қарастырамыз.Қарыз гергеқарызға берілетін A соманы есептеудіңе кітəсілін қарастырайық, есептік үстеме негізінде қарапайым жəне күрделі пайыздар схемасы бойынша есептеу. Мұндайесептеулервексельдердібанктікесепкеалғанда, ломбардтық несие бергенде жəне т.б. жағдайларда қолданылады. C жəне e мəндері белгілі, есептеу керек A соманы. Анықтама. Жылдық есептік үстеменегізінде қарапайым пайыздарсхемасыбойыншаесептеу, несиеберушіберілгенқаржының жылсайын бірдейпайыздықақшасынғанаалыпотырадыда, алолнесиеберушігеқайтарылатын C соманың E пайызынқұрайдыделінеді.Бастапқыкездебүтінсанды t = 1,2,..., n жылдарғаберілгеннесиелерсомасын A1, A2, … An депбелгілеп, қарызданушынесиеберушіденосысомаларды t = 1,2,..., n сəйкесжылдарынесиегеқолданғаныүшіннесиеберушіге (пайыздықақшасыменқоса) C соманықайтарамындегенкелісімменқарызғаалғанжəнеесептік үстеменегізінде қарапайым пайыздарсхемасыбойыншаесептегенжағдайдықарастырайық. 2.9. Анықтамабойынша: A1 = C – eC, A2 = C – (eC + eC) = C– 2eC = A1 – eC, … … … … … … … … … … An = C – (eC + eC +…) = C– neC = An–1 – eC, осыданбарып, мынадайсалдартуындайды. Салдар. Қарызгернесиеніқолданғаныүшіннесиеберушіге (пайыздықақшасыменқоса) C соманықайтарамындегенкелісіммен t = 1,2,..., n жылдарғасəйкеснесиегеберілген A1, A2, …An сомалармынақатынасарқылыанықталынып, Am = C(1 – me), m = 1,2, …, n, (2.22) оларбіріншімүшесі (C – eC) жəнеайырымы (– eC) болатын кемімеліарифметикалықпрогрессияны құрайды. Есептік үстеменегізінде қарапайым пайыздарсхемасыбойыншаесептегеннесиекезкелгенбірнеше t жылдарға (бүтінжылболуміндеттіемес) берілгенжағдайғаөтіп, жəне (2.22)қатынастытұжырымдап, келесіанықтаманыенгізейік. Анықтама. Егернесиеліккелісімдежылдық есептік үстеменегізінде қарапайым пайыздарсхемасыбойыншаесептеуқарастырылса, ондақарызданушы t жылнесиеніпайдалануүшін, несиеберушіден A(t) =C( 1– te), (2.23) соманы алады да, ал пайыздық ақшаны B=B(t) мына формулабойынша есептейді: B(t)=C – A = C – C(1– et) = Cet. (2.24)
4 ТАҚЫРЫП. КЕПІЛДІКПЕН ҚАМТАМАСЫЗДАНДЫРЫЛҒАН ССУДАЛАР(ЛОМБАРДТЫҚ НЕСИЕЛЕР). Ломбардтық несие алу үшін қарызгер несие берушігеатериалдық құндылық құрайтын заттың немесе объектінің тиісті құжатын немесе құнды қағазды кепілдік ретінде өткізуге індетті.Кепілдік құндылықты алғаннан кейін, несие беруші оның ағымдағы нарықтық құнын бағалайды да, несиелік келісім шартта,41 қарызгердің несие берушіге қайтаратын қарыз сомасы (пайыздық ақшалар жəне несие берушінің қарызға қызмет жасаудағышығындарымен қоса), кепілдікке берілген құндылықтыңбағасының (50 – 80)% аспайтыны туралы тұжырымдап, есептікүстеме негізінде қарызгерге қарапайым пайыздар схемасы бойыншассуда береді. Ломбардтық несие жалпы3 ай ерзімге беріледі, ал оны өтеукелесі нұсқалардың біреуімен жүргізіледі: 1) қарызгер барлық қарызды уақытында өтейді; 2) қарызгер қарызды өтеу ерзімін келесі3 айға созады; 3) қарызгер уақытында барлық қарыздың тек бір бөлігін төлейді де, ал қалған бөлігін өтеуді келесі 3 ай бойына созуы мүмкін. Пайыздық ақшаларды төлегенде əр айдағы нақтылы күндер есептелінеді де, ал жыл 360 күндермен теңестіріледі. Ломбардтық несиені берген жəне өтеген күндер бір күн деп есептелінеді. Егер қарызгер қарызын уақытында өтемесе, онда ол, індеттітүрде, өтеу ерзімін ұзартқан күндері үшін несие берушімен көбейтілген(айыптық) үстемемен есептеседі. Қарызгердің келіскен ерзімде несие берушімен толық есептесуге үмкіншілігі болмаған (немесе есептескісі жоқ)жағдайда, қабылданған заң бойынша несие беруші кепілдікке алынған құнды затты өз үддесіне жұмсай алады. Клиент ломбардтық несие алу үшін150 акциясын банкке кепілдікке берді. Банк акцияның80% курстық бағасының есебінен 3 айға несие беруге келісті. Жылдық есептік үстеме18%, ал3 ай бойы қарызға қызмет жасағаны үшін, банк шығыны 2000 теңге құрайды. Егер 1 акцияның ағымдағы курсы 3000 теңге болса жəне несиеге ақша банктен 16.03.010 ден 16.06.010 дейін берілсе, онда клиент банктен қанша соманы несиеге алады? Шешуі. Қаржыгердің барлық құнды қағаздарының бағасы тең: 3000 теңге 150 = 450 000 теңге, сондықтан, қарызгер банкке қайтару керек: C= 450 000 ·0,8 = 360 000 теңге. Несиені пайдаланған уақытты t(жылдар) анықтайық. Несиені 16.03.010-ден 16.06.010-дейін пайдаланған уақыт t, жылдарды (2.28) формула арқылы есептейік: t = s/g = 91/360 = 0.2528, мұндағы s = 91 күнге несие берілген жəне g= 360 жылдағы күндер саны. (2.24) формуламен(e) есептік үстемені аламыз.B = Cet = 360 000 ·0,18 ·0,2528 = 16380 теңге.Осыдан кейін қарызгердің қолына алатын сомасын табамыз. Ол үшін C= 360 000 сомадан, пайыздық ақшаны B = 16380 жəне банк шығыны2000 теңгені алып тастаймыз: A = C– B– 2000 = 360 000 – 16380 – 2000 = 341 620 теңге. Жауабы: Қарызгер банктен16.03.010 күні341 620 теңге алады жəне 16.06.08 күні360 000 теңге қайтарады. Алдыңғы есепті жалғастырып, ынадай жағдай болсын делік, қарызгер16.06.010 –де қарыздың60 000 теңгесін төлесін де, қалған бөлігін өтеу ерзімін келесі3 айға ұзартуын сұрасын. Банк есептік үстемені20% дейін көтеріп, несиенің қалған бөлігін тағы 3 айға ұзартуға келісті. Қарызгер банкке16.09.010 күні қанша ақша өтейді? Шешуі. Басында 16.06.010 қанша қарыз қалғанын анықтаймыз: A1= 360 000 – 60000 = 300 000 тенге. (2.23) формуланы пайдаланып, 91 күннен кейін30000 теңгені несие 20% есептік үстемемен (e – есептік үстеме) 16.06.010-ден 16.09.010-дейін қолданғаны үшін қарызгер қайтаратын соманыанықтаймыз:
Сонымен, қарызға жасаған қызметі үшін, банк шығынын есептеп, қарызгер16.09.010 күні банкке төлейді: 315 974,3 + 2000= 317 974,3 теңге. Жауабы: Қарызгербанкке 16.09.010 күні 317 974,3 теңгетөлеугеміндетті. Əрбірмезгілдетөленгенақшаларсомасынсалыстыру Əрезгілдетөленгенақшаларсомасынсалыстырутəсілінбаяндауғаөтпесбұрын, 1. Бекітпе. Жылдықпайыздықүстемеpнегізіндеқарапайымпайыздарсхемасыбойыншаесептеу: а) егербанккедепозиттікшотқаAсоманықазірсалсақ, ондаtуақыт(жыл) өткенненкейіншоттаынадайсомапайдаболады: C = A(1+ pt); б) депозиттікшоттаtуақыт (жыл) өткенненкейінCсомапайдаболуүшінқазіршотқаынадайсомасалукерек: A = Баяндалған1- бекітпеарқылыанықтамаенгізейік. 2.13. Анықтама. t1 және (t1 >t2 ) уақыттарғасəйкесS1, S2 сомасындайтөленгенақшалар, егердепозиттікшотқасалынғанS1 сомаt =t2– t1 уаққытөткенненкейінS2 сомағаайналса,қарапайымпайыздықүстемеpбойыншаэквивалентті(баламалы) депаталады.Қарапайымпайыздықүстемеpбойынша 1. бекітпегесəйкесS1жəнеS2 ақшасомаларықашанынадайжағдай: S= S1 (1+ p(t2– t1)) (4.30) тексондағанаэквивалентті. 2. Бекітпе. Жылдықесептікүстемеeнегізіндеқарапайымпайыздарсхемасыбойыншаесептеу: а) егербанккедепозиттікшотқаAсоманықазірсалсақ, ондаtуақыт(жыл) өткенненкейіншоттаынадайсомапайдаболады: C= б) депозиттікшоттаtуақыт (жыл) өткенненкейінCсомапайдаболуүшінқазіршотқаынадайсомасалукерек: C = A(1– et). Баяндалған3-бекітпеарқылыанықтамаенгізейік. Анықтама. 4. Бекітпе. Жылдықесептікүстемеeнегізіндекүрделіпайыздарсхемасыбойыншаесептеу: а) егербанккедепозиттікшотқаAсоманықазірсалсақ, ондаtуақыт(жыл) өткенненкейіншоттаынадайсомапайдаболады: A= б) депозиттікшоттаtуақыт (жыл) өткенненкейінCсомапайдаболуүшінқазіршотқаынадайсомасалукерек: C = A(1– e)t Баяндалған4-бекітпеарқылыанықтамаенгізейік. Е с к е р т п е. $2000 соманы $2500 сомамен (t1= 0) уақытмезгілінде салыстырып, есепті басқаша шығаруға болады. 4.13. Күрделі пайыздық үстеме 6%. Қандай сома көп: $2000 соманы қазір (t2= 0) төлеген бе немесе $2030 соманы (t2= 0,5)жылдан кейін төлеген бе? Шешуі. $2500 соманы (t2= 0,5) жылдан кейін төлеген $2000соманың эквивалентті сомасымен салыстырамыз. Ол үшін $2000соманы S1 белгілеп, (2.31) формула арқылы күрделі пайыздықүстеме0,06 бойынша осы сомаға эквивалентті S2 соманы табамыз. Жауабы. Қазір(t2= 0) төлеген$2000 сома көп. 4.14. Қарапайым есептік үстеме6%. Қандай сома көп: $2000соманы қазір (t1= 0) төлеген бе немесе $2030 соманы (t2= 0,5)жылдан кейін төлеген бе? Шешуі. $2000 соманы S1 белгілеп, (2.32) формула арқылы қарапайым есептік үстеме0,06 бойынша осы сомаға эквивалентті S2 соманы табамыз. S2= Жауабы. Қазір(t1= 0) төлеген$2000 сома көп. А н ы қ т а м а. Келешекте төленетін соманың қазіргікездегі шамасы немесе келтірілген сома мəні, оған (t = 0) уақыт мезгілінде эквивалентті мəн деп аталады.
5 ТАҚЫРЫП. ПАЙЫЗДЫҚ ҮСТЕМЕ НЕГІЗІНДЕ ҮЗДІКСІЗ ПАЙЫЗДАР СХЕМАСЫ БОЙЫНША ССУДА БЕРУ. Мынадай жағдайларда үздіксіз пайыздар деген ұғымы қолданылады: қарапайым пайыздарды жылдық пайыздық үстемегеp арттыру келісімімен, клиент банкпен A соманы депозиттік шотқа, жылдың 1/m – бөлігіне тең ерзімге дейін салуға шарт жасасты делік. Осы ерзім өткеннен кейін (2.12) формула бойыншадепозиттік шотта- рынадай сома пайда болады: С = A(1+ оны клиент шоттан алады да, сол шотқа қайта салады (пайызбенқоса соманы реинвестрлейді). Нəтижесінде, жылдың«екінші» 1/m– бөлігі өткеннен кейін депозиттік шотта ынадай сома пайда болады: С = A(1+ оны клиент ерзімі өткеннен кейін тағы да шоттан алады да, сол шотқа қайта салады. Осы процедура бір жыл бойы m–рет қайталанады да, клиенттің депозиттік шотында ынадай сома пайда болады: С = A(1+
Мынадай m= 12 жағдайда пайыздық ақшаны реинвестрлеу ай сайын, m= 365 күн сайын, m= 365·24 = 8760 сағат сайын жүреді. Минут сайын, секунд сайын жəне шексіз жағдайда m ∞ →пайыздарды үздіксіз реинвестрлеуді теориялық тұрғыда қарастыруға болады. Сондықтан, егер (2.35) формулада шектеугеөтсек, онда ына жағдайда m ∞ → төмендегідей қатынас алынады: C = ол депозит ерзімі 1 жылға тең болған жағдайдағы, жылдық пайыздық үстеме p негізінде пайыздарды үздіксіз арттыру формуласын көрсетеді. Депозит ерзімі t жылға тең болған жағдайдағы, жылдық пайыздық үстеме p негізінде пайыздарды үздіксіз арттыру формуласының түрі: C=Aept (5.5) Е с к е р т п е. (5.4) жəне (5.5) формулалардағы e натуралдық логарифм негізі. Пайыздарды үздіксіз арттыру формуласын, дифференциалдық теңдеулерді қолданып, басқаша тəсілдермен алуға болады. Осы ақсатпен келесі ысалды қарастырайық. 5.1 Банктегі салымның өсу жылдамдығы салым өлшеміне пропорционалды өзгереді, пропорционалдық коэффициенті 0,03. Егер салымның алғашқы сомасы10000 (ақша бірлігі) болса, салым уақыт бойынша қандай заңдылықпен өзгереді жəне шотта2 жылдан кейін қандай сома болады? Шешуі. t уақыт езгілінде салым өлшемі ынадай A=A(t) болсын. Алғашқы салым сомасы10000, ал уақыт бойынша салым туындысы
Оның бастапқы шарты: A(t=0)=10000. (5.7) Дифференциалдық теңдеулер курсынан белгілі, (5.6) жəне (5.7) қатынастар Коши есебін шешуге сəйкес, яғни оны мына түрде жазуға болады: А(t) = 10000e0.03t сөйтіп, 2 жылдан кейін шотта ынадай сома болады: . А(t) = 10000e0.03*2 = 10000e0.06 =10000*1.06=10600 Жауабы. Салымның уақыт бойынша өзгеру заңдылығының түрі: А(t) = 10000e0.03t, ал 2 жылдан кейін шоттағы сома: 10600 ақша бірлігіне тең. Ссудалардың нығаюы. Несие беруші бірдей бір уақытта қаржыгерге жылдық пайыздық үстемесін p1,p2 … pn, қарапайым пайыздар схемасымен,t1,t2 , …, tn мерзімге, A1,A2 …, An өлшемді n ссудалар берді делік. Қаржыгер барлық қарызын бірден төлемекші, ссудаларын нығайтпақшы. Қаржыгер де, несие беруші де шығынға ұшырамауы үшін, қаржыгер қанша уақытта барлық қарызын бірден төлей алады? Барлық ссудаларды жылдық пайыздық үстемесі p қарапайым пайыздар схемасымен t ерзімге (жыл) берілген бір A ссудаға айырбастауға болатыны үмкін болсын. t ерзімі ссудаларды нығайту ерзімі деп аталады. Нығайту төлемін төлеп біткеннен кейін, A, p жəне t мəндерін табу үшін қарызгердің ынадай істер жасау керектігін аңғарамыз: 1) барлық қарыздар сомасын өтеу; 2) əр ссудаларды қолданғаны үшін пайыздық ақшаларын өтеу. Сонымен, екі қатынас орындалуға тиіс: A1+ A2 + …+ An =A, (5.8) A1 p 1 t1 + A2 p 2 t2 +…+ An p n tn= Apt (5.9)
Егер (5.8) формуладан (5.9) формулағатеңдеуінқойсақ, ондаынақатынасалынады: A1 p 1 t1 + A2 p 2 t2 +…+ An p n tn=(A1+ A2 + …+ An)pt (5.10) осыданбарып, жалпыссуданыңнығайтуерзімінтабамыз: A= (5.11) формуланықолданыпекіқарапайымжағдайдықарастырайық. 1. Ж а ғ д а й. Барлық ссудалар A бірдей өлшерде жəне олар бірдей пайыздық үстемелермен p берілген. Онда, (5.11) формуладан ынадай қатынас туады: t= 2. Ж а ғ д а й. Барлық ссудалар əртүрлі өлшерде жəне əртүрлі мерзімге, сонымен қатар бірдей пайыздық үстемелермен p берілген. Мұндай жағдайда, (5.11) формуладан мынадай қатынас туады: t= 5.17. Несие беруші жылдық пайыздық үстеме 16%–бен қарапайым схема бойынша бір қарызгерге үш ссуда берді. Ссуданыңпараметрлері2.2 кестедекөрсетілген. 2.2–кесте. Ссудатуралы əліметтер
Қарызгер үшінші (№3) ссуданы алғаннан кейін барлық ссудаларды нығайтпақшы. Өтеуді нығайту күнін жəне қаржыгер несие берушіге осы күні қандай сома төлейтінін анықтау қажет? Шешуі. Ссудалар əртүрлі уақыт езгілінде берілуіне байланысты, есепті шешу үшін бірден (9.6) формуланы пайдалануға болмайды. Басында барлық төлемді бірдей уақыт 51 мезгіліне келтіреміз. (2.30) жəне (2.28) формулалар бойынша, 11.06.08 төленген1 000 000 теңге сомаға(№1 ссуда), қарапайым пайыздық үстеме16% бойынша эквивалентті сома: 1000000=(1+0.16 07.08.08 төленген. 5.3-кестеде қарызгердің қарыздарымен жасаған ситуациялары келтірілген 5.3-кесте Қарызгердің07.08.08 күнгі қарыздары
07.08.08 сəйкесінше S1= 33 күн, S2= 41 күн жəне S3=120 күндерге тең ерзімге берілгенін анықтаймыз. Сондықтан: t =
мұнда s – ссудаларды нығайту күндері. (5.14) формуладағы өрнекті (5.13) формулаға қойып, аламыз: t =
Сөйтіп, s =105 күн. Енді өтеуді нығайту күнін табуға болады: 07.08.08 +105 күндер=20.10.08. Жауабы. Қарызданушы 10.10.08 күні негізгі қарызы (1 000 000 + 2 000 000+ + 7 000 000) =10 000 000 теңге) ен қоса əр ссуда өлшерін толық мерзім бойы(№1 ссуда: 10.09.08 – 11.06.08 = 90 күндер, №2 ссуда: 19.10.08 – 20.07.08 = 90 күндер жəне №3 ссуда: 06.12.08 – 07.08.08 = 120 күндер) қолданғаны үшін пайыздық ақшаларын несие берушіге төлеуге тиіс:
10 000 000 + 485 245,82=10 485 245,82 теңге.
6 ТАҚЫРЫП. ССУДАЛАРДЫ ӨТЕУ СХЕМАСЫ
|

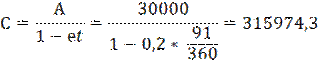
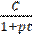
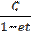
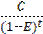
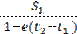 =
= 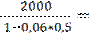 =
= 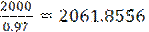 ˃2030
˃2030 ) (5.1)
) (5.1)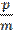 )m (5.3)
)m (5.3)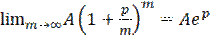 (5.4)
(5.4)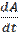 , салым өсуінің жылдамдығы болғандықтан, салымның уақыт бойынша өзгеру заңдылығы мына диффренциалдық теңдеуді шешумен анықталады:
, салым өсуінің жылдамдығы болғандықтан, салымның уақыт бойынша өзгеру заңдылығы мына диффренциалдық теңдеуді шешумен анықталады: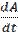 =0,03A (5.6)
=0,03A (5.6)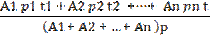 (5.11)
(5.11)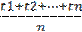 (5.12)
(5.12) (5.13)
(5.13)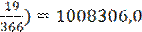 теңге
теңге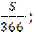 t1=
t1= 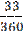 t2=
t2= 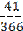 t3=
t3= 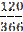 (5.14)
(5.14)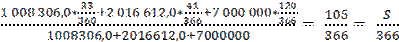 күн
күн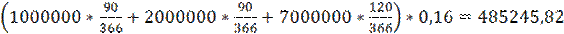 теңге. Сонымен, жалпы төлейтін ақша сомасы:
теңге. Сонымен, жалпы төлейтін ақша сомасы:


