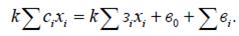Есіңізде болсын!

Мастер функцияны қолданбай, бірден формуланы енгізуге болады.

 

 

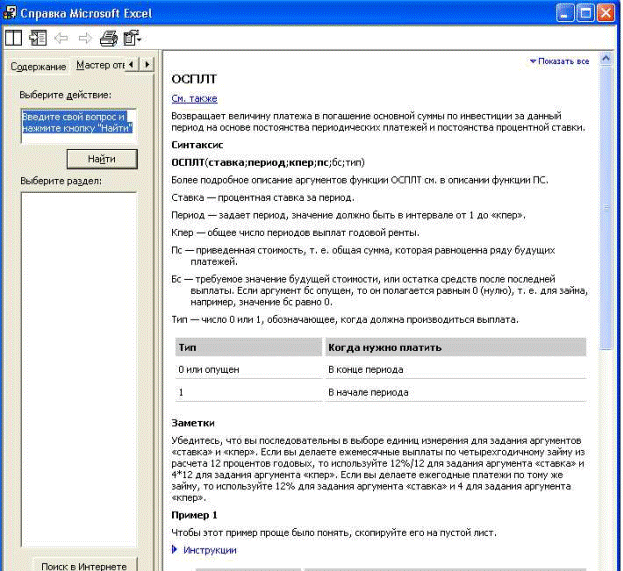
7.3-сурет. Қаржылық функциялармен жұмыстар жүргізу бойынша анықтама

 

Қаржылық фукциялардың аргументтерін дəйектегенде мыналарды есте ұстаған жөн:

· ақша қаражаттарының шығындарын бейнелейтін барлықаргументтер (мыслға, əрбір жылдардағы төлемдер), теріс сандар арқылы, ал келіп құйылатын, ақша қаражаттарын өсіретін (мысалға,дивиденттер) – оң сандар мен көрсетіледі;

· функциялар аргументтері сияқты барлық күндер десандық формата көрсетіледі;

· логикалық аргументтер үшін истина немесе ложь,əйтбесе Логические функция категориясы қолданылады;

· əрбір аргумен өзінің орнында болуға тиіс! Егераргументтер босқалдырылса, онда бөліп тұратын белгілер саныотырғызылады.

Мысал. Егер жылына 12 % үстемемен 5 жыл мерзімге 1000000 000 теңге мөлшерінде ссуда берілсе жəне негізгі төлемдітөртінші жылы қайтару мүмкіншілігі туса, онда ақша қаншамөлшерде төленуге тиіс?

Шешімі. Əрбір есеп айру аралықтың басында немесе аяғында займбойынша өтелетін, негізгі төлемдер үшін MS Excel-де мынадайфункция қолданылады:

ОСПЛТ (Ставка, Период, Кпер, Пс, БС).

Ескерту: MS Excel-дің бұрынғы версияларында бұл функцияОСНПЛАТ деп аталды.

 

7.4-сурет. Жұмысшы бетте қаржылық функцияның негізгі аргументтері

 

Біздің жағдайда ОСПЛТ функциясының түрі:

ОСПЛТ (12%, 4, 5, 1000 000 000)

Деректерді енгізу жəне есептеулер 7.4-суреттегі мəліметтергесəйкес жүргізіледі.D8 – ші ұяға мына формула енгізіледі:

= ОСПЛТ (D5, D6, D4, D3)

7.5-сурет. Займ бойынша негізгі төлемдерді есептеу

 

Нəтижесінде D8 – ші ұяда 5 жылға 12% үстемемен алынғанссуданы 4-ші жылы 221 149 339, 88 теңге мөлшерінде төлеукеректігін анықтаймыз.

Мысал. Жылдық 10% үстемемен бастапқы взносы 25%350 000 мың теңге 20 жылға ипотекалық ссуда берілген. Осыссуданың айсайынғы жəне жылсайынғы төлемін есептеңіз.

Шешімі. Тұрақты пайыздық үстемеде тұрақты аралықтарда төленетін

шамаларды есептеу үшін (мысалға, займ бойынша тұрақтыаралықтарда төлеп отыру), ПЛТ функциясы (функцияның бұрынғыверсияларында – ППЛАТ) қолданылады: ПЛТ(Ставка; Кпер; Бс; Пс; Тип) Біздің жағдайда ПЛТ функциясының түрі:

ПЛТ(10%/12; 20*12; - (350000*(1-25%))) – айсайынғытөлемдер;

· ПЛТ(10%; 20; - (350000*(1-25%))) – жылсайынғытөлемдер.

Есепті шешіу барысында қолданған формулалар 7.6-суреттекелтіріліп, 7.7- суретте есептің шешім нəтижесі берілді.

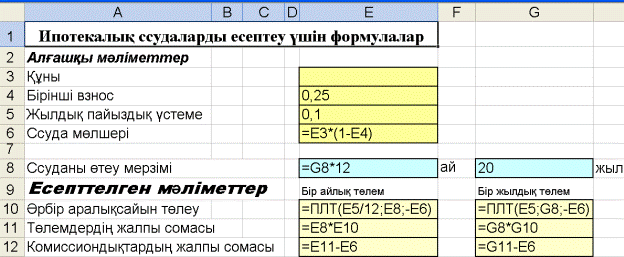
7.6-сурет. Ипотекалық ссудаларды есептеу үшін формулалар

 

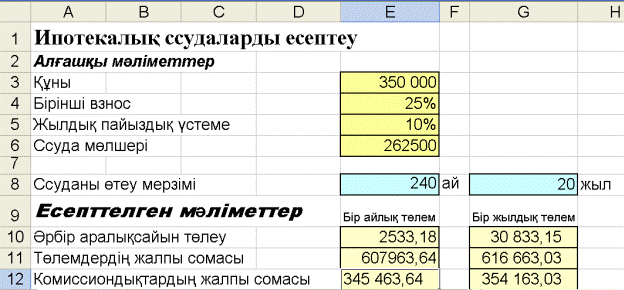
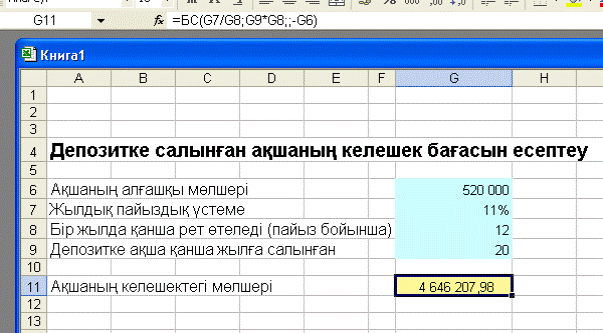
7.7-сурет. Ипотекалық ссудаларды есептеу нəтижесі

Мысал. Егер 520 000 теңге 11% жылдық үстемемен 20жылға салынса, онда сіздің есеп-шотыңызда қанша сомаболатынын анықтаңыз. Айсайын пайыздық үстеме есептелініпқосылады.

Шешімі. Үстемемен салынған соманың келешектегі бағасын есептеуүшін күрделі пайыздар схемасы қолданылады. Оның есептікформуласы мынадай БС функцияға (бұрынғы версияда – функцияБЗ) негізделген:

БС(Ставка; Клер; Плт; Пс; Тип)

Біздің есеп үшін БС функциясының түрі: БС(11%/12; 20*12;; -520 000)

Есептің Excel – дегі 7.8-суретте келтірілген. Мұндағы G11ұяда мынадай формула жазылады:=БС(G7/G8;G9*G8;;-G6).

Осы формула f x - мастер функция жолында да көрсетіліп тұр(7.8-суретті қараңыз).

 

 

7.8-сурет. Салымның келешектегі бағасын есептеу

 

15 ТАҚЫРЫП. ҚАРЖЫЛЫҚЕСЕПТЕРДІҢМОДЕЛЬДЕРІ.

 

Тəжірибеде басқа оңтайластыру есептеріне қарағанда жиібайқалатын, көптеген жағдайларда оңтайлы шешім қабылдаудықажет ететін əртүрлі қаржылық есептерін кездестіруге болады.Шындығында, есепті шешу нəтижесінің критериясы максимумге,мысалға, пайда, табыс жəне тағы басқа немесе минимумге, мысалға, өзіндік құн, өнімнің бағасы жəне тағы басқада көрсеткіштерізделінетін барлық оңтайластыру есептері, қаржылық есептерінежатады. Сонымен қатар кəдімгі қаржылық есептерге, шығынсыз-

дық (зиянсыздық) нүктені есептеу, капиталды іске салуды жоспарлау, инвестициялау портфельдерін қалыптастыру, ақша ағымынбасқару жəне басқа да қаржы айналымына байланысты есептердіжатқызады.Соныменқатаркəдімгіқаржылықесептерге, шығынсыздық (зиянсыздық) нүктеніесептеу, капиталдыіскесалудыжоспарлау,инвестициялаупортфельдерінқалы

птастыру, ақшаағымынбасқаружəнебасқадақаржыайналымынабайланыстыесептердіжатқызады.

Қаржылықесептердіңматематикалықмодельдерісызықтық,сызықтыемес, бүтінсанды, екілікайнымалыларменжəнебасқадатүрде, соныменқатарөзініңқұрамыбойыншаөндірістік, қоспаесебісияқты, транспорттықтиптес, тағайындауесебінеұқсасжəнебасқадатиптеболуымүмкін. Соныменқатар, қаржылықесептерініңөздерінетəнайрықшылықтарыболады. Олардыңмағынасындауақытанықбайқалыптұрады. Мысалға, уақытбойыншашамаларыбірқалыптыемес, капиталсалымынжоспарлағанданемесеақшаағымынбасқарғандапайыздықүстемеесептелінеді.Бірақосығанқарамастанқаржылықесептер, динамикалықемес,міндеттітүрдестатистикалықделінеді, яғнибасқашаайтсақ,мұндаймодельдерде, уақыттəуелсізайнымалыемес, əйтеуірбірпараметріретіндеескеріледі.Жұмысбарысындақаржылықесептерменкезкелгенкəсіпкернемесекəсіпорынжетекшісініңжиіайналысуынатуракелетінісөзсіз. Сондықтанкелесітақырыптардатəжірибедежиікездесетін, біршамақызықтықаржылықесептерінқарастырамыз.

Шығынсыздықтыталдау. Экономикада шығынсыздықты (зиянсыздықты) талдау маңызды мəселе. Шығынсыздықты талдау барысында, жаңа өндірістіұйымдастыру үшін, қанша қаржы керектігі бағаланады жəне жаңаөнімді өндіру үшін іске салынатын капитал туралы жан-жақтыталдаулар жасалынады. Жаңа өнімді өндіруге кеткен барлықшығындардың сомасы жəне оған қосылған бастапқы кезде осыөндірісті іске қосу үшін салынған капитал мөлшері мен өнімдінарыққа шығарып, сатқанда алынған барлық табыстардыңсомасы тең болатын уақыт аралығы ізделінеді. Сонымен қаншауақыт мөлшерінде өндіріс шығынсыз нүктеге жететіні, яғни шығынжəне кіріс тең болатын уақыт анықталынады.

Өнім өндірілмейтін халық шаруашылығының кейбір салаларында, мысалға, сауда-сатық салада немесе тұтынушыларға қызмет көрсету орындарында шығынсыз нүкте – рентабельдіктің табалдырығы (орысша - порог рентабельности) деп аталады.

Есептің мағынасы түсінікті жəне қарапайым болу үшін өндірісті іске қосуға салынған алғашқы капитал мөлшері белгілі депесептейік.Айталық, бір кəсіпорын n жаңа Б₁, Б₂,…,Бn деп аталатынбұйымдарды шығаруды жоспарлап отыр делік. Бұйымдардың əрқайсысын алдын-ала жобаланған шамада шығару үшін в₁, в ₂,..., в_п мөлшерде бастапқы капиталды іске салу керек болсын. Бұлкапиталдар бекітілген немесе тұрақты деп аталатын шығындаржəне олардың шамалары алдыңғы уақыттарда бұйымдардың өндірумөлшерінің дамуымен байланысы болмайды. Негізінде бұл шығындарға, алғашқы құралдарды сатып алуға, оларды жұмысқа қосуға

кеткен жəне т.б. жұмыстар үшін керекті шығындар жатады. Осышығындармен қатар, өндірісте өнімдер түрлеріне байланыстыбөлінбейтін жалпы в ₀ мөлшерде бекітілген шығын болуы мүмкін.Мысалға, кəсіпорында барлық бұйымдарды өндіруге қатысы бар,жаңа цех құрлысының бағасы (в 0) немесе т.б.с.с.

Əрбір жаңа Б₁, Б₂,…,Бn бұйымдардың бір данасының өзіндікқұны (з₁, з₂,...,зn) жəне нарықта қаншадан (с₁, с₂,..., с n) сатылатыныалдын-ала анықталған деп есептейік. Сөйтіп, шығынсыздықтыталдауға керекті деректердің манимальды жиынын атап өттік.

Кəсіпорын Б₁, Б₂, …, Бn деп аталатын бұйымдарды, белгілібір уақыт аралығында (бір айда, тоқсанда, жарты жылда немесе біржылда), x₁, x,..., x n данадан өндіреміз деп жоспарласа, онда осыөнімдерді өндіруге кеткен барлық шығындардың сомасы (қосылғанбастапқы өндірісті іске қосу үшін салынған капитал мөлшері) меноны нарыққа шығарып сатқандағы барлық табыстардыңсомасы теңболатын k уақытты арқылы шығынсыздықтың теңдігі құрылады.

Бұл теңдікті былай жазыуға болады:

Осы теңдіктен шығынсыз нүктеге жететін уақыттыанықтаймыз:

 

Негізінде өндірістің мақсаты шығынсыздық нүктедегі өнді-

рілетін өнімдердің мөлшерін (x 1, x 2,..., x n) анықтау жəне бұл

өндіріс деңгейінде қызықты мəселе. Мұндай жағдайда шығынсыз

нүктеге жететін уақыт аралығы бірге теңестіріледі (k =1) де, нəти-

жесінде шығынсыздықтың теңдеуін мына түрге айналдырады:

 ci xi зi xi в вi 0

немесе

() . ci зi xi в 0 вi (8.2)

Көп өнімді есептер үшін мұндай теңдеулердің шексіз ше-

шімдері болуы əбден мүмкін, ал жалғыз ғана өнімді есептерде бір-

ақ шешімі болады. Көп өнімді есептерді шығару үшін қосымша

шарттар енгізіледі. Мұндай шарттарда көбінесе шығынсыз нүктеге

жеткенге дейінгі айнымалы шығындардың минимальды немесе

пайданың максимальды болуын көздейтін, белгісіздердің мəндерін

анықтайды.

Есепті аталған мақсаттарда шығаратын болсақ, бірінші

жағдайда шығынсыз нүктеге жеткізуге кеткен қаржылық шығын

азаяды. Бірақ шығынсыз нүктеге жететін уақыт ұзарады. Екінші

жағдайда шығынсыз нүктеге жетуге кеткен уақыт азаяды. Бірақ

шығынсыз нүктеге жеткізуге кеткен қаржылық шығын көбейеді.

Оңтайлы өндірістік жоспарды анықтағаннан кейін, осы

жоспарды орындау мерзімі сияқты шығынсыздық нүктеге жету

мерзімі есептелінеді.

Шығынсыз нүктеге жету үшін, өндірістің оңтайлы жоспары

анықталатын есептің математикалық моделін құрамыз. Математи-

калық модельді жазуға керекті белгілер толығымен белгілі, атап

айтсақ:

– Б1, Б2, …, Бn – бұйымдарының оңтайлы мөлшерлерін көр-

сететін: x 1, x 2,..., x n – айнымалылары;

– бұйымдардың өзіндік құны (з 1, з 2,..., з n) жəне олардың

сатылатын бағалары (с 1, с 2,..., с n);

– бұйымдардың əрқайсысын өндіруге қажетті бастапқы ка-

питалдар в 1, в 2,..., в n –мөлшері жəне т.б.

Егер өндірістік оңтайлы жоспар құру үшін айнымалы шы-

ғындардың минимальды болу шарты қарастырылса, онда мақсат

функция мына түрде жазылады:

⇒min i i Z з x (8.3)

Егер өндірістік оңтайлы жоспар максимальды пайда алу

шартына есептелінсе, онда мақсат функция мына түрде жазылады:

⇒max i i Z c x (8.4)

Шектеу ретінде шығынсыздықтың теңдеуі алынады:

() . ci зi xi в 0 вi (8.5)

Сонымен есептің математикалық моделін құрдық. Тəжірибе-

лік есептерді шығарғанда нақтылы өндірістің жағдайларына байла-

нысты басқада шектеулер құрылуы мүмкін. Мысалға, өндіріс қуа-

тының немесе қорларының шектеулігіне, қала берді нарық сұра-

нысына байланысты жаңадан бірнеше шектеулер қарастыруға

болады.

8.1.1 Жаңа ұйымдастырылып жатқан нақтылы өндірістің;