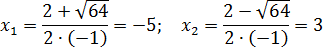Решение уравнений и систем уравнений
Уравнение вида ax=b, где x- переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной. Пример, 4(x+7)= 3 - x 4x + 28= 3 – x 4x+x= 3 -28 5x = -25 x = -25:5 x= -5 Линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где x и y – переменные, a, b и c - некоторые числа. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Пример,
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0. Находим дискриминант D = b2 − 4ac. · Если D < 0, корней нет; · Если D = 0, есть ровно один корень; · Если D > 0, корней будет два. Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Пример: Решить квадратные уравнения: 1. x2 − 2x − 3 = 0; 2. 15 − 2x − x2 = 0; 3. x2 + 12x + 36 = 0. Решение: Первое уравнение: D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение: D > 0 ⇒ уравнение снова имеет два корня. Найдем их:
Наконец, третье уравнение: D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Ответ: 1) x1 = 3; x2 = -1; 2) x1 = −5; x2 = 3; 3) x = −6.
Решим дробное рациональное уравнение x – 3 1 x + 5 Решение: Находим общий знаменатель. Это x(x – 5). Итак: x2 – 3х x – 5 x + 5 Теперь снова освобождаемся от знаменателя, поскольку он одинаковый для всех выражений. Сводим подобные члены, приравниваем уравнение к нулю и получаем квадратное уравнение: x2 – 3x + x – 5 = x + 5 x2 – 3x + x – 5 – x – 5 = 0 x2 – 3x – 10 = 0. Решив квадратное уравнение, найдем его корни: –2 и 5. Проверим, являются ли эти числа корнями исходного уравнения. При x = –2 общий знаменатель x(x – 5) не обращается в нуль. Значит, –2 является корнем исходного уравнения. При x = 5 общий знаменатель обращается в нуль, и два выражения из трех теряют смысл. Значит, число 5 не является корнем исходного уравнения. Ответ: x = –2
|

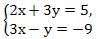 выразим из второго уравнения y=3x+9, получим
выразим из второго уравнения y=3x+9, получим