Неравенства вида 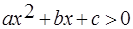 ,
,  ,
, 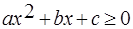 ,
, 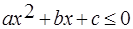 , где
, где 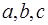 – заданные числа, причем
– заданные числа, причем  , называются квадратными неравенствами или неравенствами второй степени. Основной метод решения таких неравенств – метод интервалов. Если дискриминант квадратного уравнения
, называются квадратными неравенствами или неравенствами второй степени. Основной метод решения таких неравенств – метод интервалов. Если дискриминант квадратного уравнения 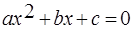 положительный, то квадратный трехчлен можно разложить на множители
положительный, то квадратный трехчлен можно разложить на множители  , где, и проверить знак выражения в промежутках, на которые разбивают действительную ось найденные значения корней. Если дискриминант квадратного уравнения отрицательный, то квадратный трехчлен не меняет знак ни при каких действительных значениях переменной. Если
, где, и проверить знак выражения в промежутках, на которые разбивают действительную ось найденные значения корней. Если дискриминант квадратного уравнения отрицательный, то квадратный трехчлен не меняет знак ни при каких действительных значениях переменной. Если  и
и  , то
, то 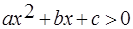 для всех
для всех 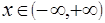 . Если
. Если 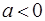 и
и  , то
, то  для всех
для всех 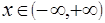 . Если дискриминант квадратного трехчлена равен нулю, то выражение
. Если дискриминант квадратного трехчлена равен нулю, то выражение 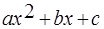 представляет собой полный квадрат и, в зависимости от знака
представляет собой полный квадрат и, в зависимости от знака 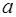 , принимает либо только неотрицательные, либо только неположительные значения.
, принимает либо только неотрицательные, либо только неположительные значения.
Пример. Решить неравенство 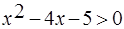 .
.
Решение. Найдем корни квадратного трехчлена: 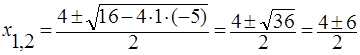 ,
,  ,
, 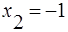 . Неравенство можно записать в виде
. Неравенство можно записать в виде 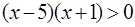 . Обозначим на числовой оси точки
. Обозначим на числовой оси точки 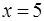 ,
,  и проверим знак выражения
и проверим знак выражения 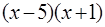 в промежутках, на которые разбивают действительную ось найденные значения корней. Если
в промежутках, на которые разбивают действительную ось найденные значения корней. Если  , то
, то 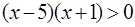 ; если
; если 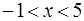 , то
, то 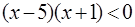 ; если
; если 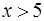 , то
, то 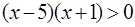 . Поэтому решением неравенства будут значения переменной
. Поэтому решением неравенства будут значения переменной 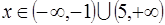 .
.
Ответ: 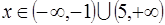 .
.
Пример. Решить неравенство  .
.
Решение. Найдем дискриминант квадратного трехчлена: 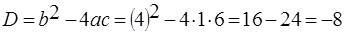 . Поскольку
. Поскольку  ,
,  , то квадратный трехчлен положителен при всех действительных значениях переменной
, то квадратный трехчлен положителен при всех действительных значениях переменной  .
.
Ответ: 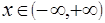 .
.
Пример. Решить неравенство 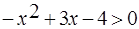 .
.
Решение. Найдем дискриминант квадратного трехчлена: 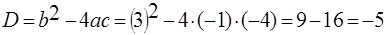 . Поскольку
. Поскольку  ,
, 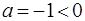 , то квадратный трехчлен отрицателен при всех действительных значениях переменной
, то квадратный трехчлен отрицателен при всех действительных значениях переменной  , то есть выражение
, то есть выражение  всегда меньше нуля, а исходное неравенство не имеет решений.
всегда меньше нуля, а исходное неравенство не имеет решений.
Ответ: неравенство не имеет решений.
Пример. Решить неравенство 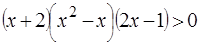 .
.
Решение. Второй из сомножителей в приведенном неравенстве не является линейным. Поэтому разложим выражение 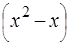 на множители:
на множители:  . Перепишем исходное неравенство в виде
. Перепишем исходное неравенство в виде 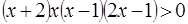 . Отметим на действительной оси корни многочлена
. Отметим на действительной оси корни многочлена  , то есть те значения переменной
, то есть те значения переменной  , при которых сомножители обращаются в нуль:
, при которых сомножители обращаются в нуль: 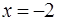 ,
, 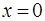 ,
,  ,
,  . В интервалах
. В интервалах 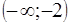 ,
, 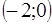 ,
, 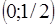 ,
,  ,
, 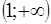 определим знак многочлена
определим знак многочлена  , подставляя вместо переменной
, подставляя вместо переменной  произвольные значения из интервалов. Решением неравенства будут те интервалы, в которых выражение принимает положительные значения
произвольные значения из интервалов. Решением неравенства будут те интервалы, в которых выражение принимает положительные значения


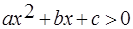 ,
,  ,
, 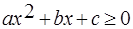 ,
, 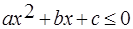 , где
, где 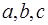 – заданные числа, причем
– заданные числа, причем  , называются квадратными неравенствами или неравенствами второй степени. Основной метод решения таких неравенств – метод интервалов. Если дискриминант квадратного уравнения
, называются квадратными неравенствами или неравенствами второй степени. Основной метод решения таких неравенств – метод интервалов. Если дискриминант квадратного уравнения 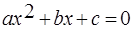 положительный, то квадратный трехчлен можно разложить на множители
положительный, то квадратный трехчлен можно разложить на множители  , где, и проверить знак выражения в промежутках, на которые разбивают действительную ось найденные значения корней. Если дискриминант квадратного уравнения отрицательный, то квадратный трехчлен не меняет знак ни при каких действительных значениях переменной. Если
, где, и проверить знак выражения в промежутках, на которые разбивают действительную ось найденные значения корней. Если дискриминант квадратного уравнения отрицательный, то квадратный трехчлен не меняет знак ни при каких действительных значениях переменной. Если  и
и  , то
, то 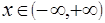 . Если
. Если 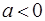 и
и 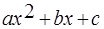 представляет собой полный квадрат и, в зависимости от знака
представляет собой полный квадрат и, в зависимости от знака 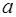 , принимает либо только неотрицательные, либо только неположительные значения.
, принимает либо только неотрицательные, либо только неположительные значения.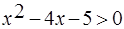 .
.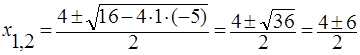 ,
,  ,
, 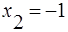 . Неравенство можно записать в виде
. Неравенство можно записать в виде 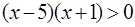 . Обозначим на числовой оси точки
. Обозначим на числовой оси точки 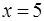 ,
,  и проверим знак выражения
и проверим знак выражения 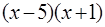 в промежутках, на которые разбивают действительную ось найденные значения корней. Если
в промежутках, на которые разбивают действительную ось найденные значения корней. Если  , то
, то 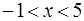 , то
, то 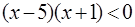 ; если
; если 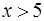 , то
, то 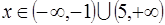 .
. .
.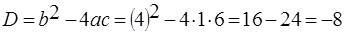 . Поскольку
. Поскольку  , то квадратный трехчлен положителен при всех действительных значениях переменной
, то квадратный трехчлен положителен при всех действительных значениях переменной  .
.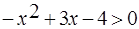 .
.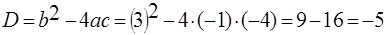 . Поскольку
. Поскольку 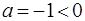 , то квадратный трехчлен отрицателен при всех действительных значениях переменной
, то квадратный трехчлен отрицателен при всех действительных значениях переменной  всегда меньше нуля, а исходное неравенство не имеет решений.
всегда меньше нуля, а исходное неравенство не имеет решений.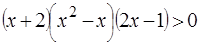 .
.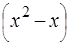 на множители:
на множители:  . Перепишем исходное неравенство в виде
. Перепишем исходное неравенство в виде 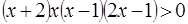 . Отметим на действительной оси корни многочлена
. Отметим на действительной оси корни многочлена  , то есть те значения переменной
, то есть те значения переменной 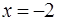 ,
, 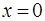 ,
,  ,
,  . В интервалах
. В интервалах 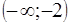 ,
, 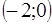 ,
, 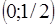 ,
,  ,
, 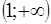 определим знак многочлена
определим знак многочлена 



