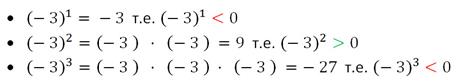При возведении нуля в натуральную степень получается ноль.

Рассмотрим примеры возведения в степень отрицательных чисел.

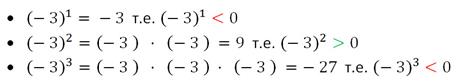
Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётную степень, - число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть: a² ≥ 0 при любом a.

o 2 • (- 3)² = 2 • (- 3) • (- 3) = 2 • 9 = 18

o - 5 • (- 2)³ = - 5 • (- 8) = 40

Свойство № 1
Произведение степеней При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a^m • aⁿ = a^{m + n}, где a - любое число, а m, n - любые натуральные числа.

Свойство № 2
Частное степеней При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a^m • aⁿ = a^{m - n}, где a - любое число, не равное нулю, а m, n - любые натуральные числа такие, что m > n.

Свойство № 3
Возведение степени в степень При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(aⁿ)^m = a^{n • m}, где a - любое число, а m, n - любые натуральные числа.

Свойства 4
Степень произведения При возведении степени в степень произведения в эту степень возводится каждый множитель и результаты перемножаются.
(a • b)ⁿ = aⁿ • bⁿ, где a, b - любые рациональные числа; n - любое натуральное число.

Свойства 5
Степень частного (дроби) Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b)ⁿ = aⁿ: bⁿ, где a, b - любые рациональные числа, b ≠ 0, n - любое натуральное число.