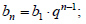Формула суммы n-первых членов арифметической прогрессии
Пример 1. Задана арифметическая прогрессия, где пятый и десятый члены равны соответственно 38 и 23. Найти пятнадцатый член прогрессии и сумму ее десяти первых членов.
Пример 2. Найти число
Пример 3. Найти число
Геометрической прогрессией называется числовая последовательность задаваемая двумя параметрами b, q (q ≠ 0) и законом Число § Если q > 0 все члены геометрической прогрессии имеют один и тот же знак, совпадающий со знаком числа b. § Если q < 0 знаки членов геометрической прогрессии чередуются. § В случае -1 < q < 1 прогрессию называют бесконечно убывающей геометрической прогрессией. Любой член геометрической прогрессии может быть вычислен по формуле:
Формула знаменателя геометрической прогрессии:
|
членов арифметической прогрессии 5,14,23,..., 
, если ее 
, 
, 
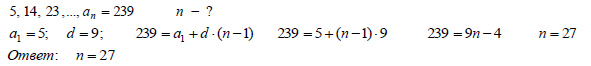
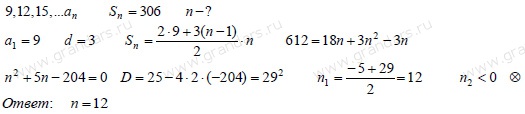
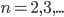
называют знаменателем данной геометрической прогрессии.
