Значения коэффициента t
Исходя из того, что все звенья размерной цепи должны иметь примерно одинаковый квалитет, находим величину к –количество единиц допуска.
Пример: Проведем расчет той же размерной цепи, изображенной на рис. 27, методом неполной взаимозаменяемости. Примем допустимый процент риска Р = 2,1 % (tD = 2,3). Предположим, что отклонения всех деталей распределены по закону Симпсона, тогда lj2 = 1/6. По формуле (6) получим Предельные отклонения звеньев А1 и А2 назначаем как и в предыдущем методе по ±IT/2 и h соответственно. Предельное отклонение звена А3 рассчитываем на основе зависимости:
где СD - середина координаты поля допуска замыкающего звена; Сj – координаты середин допусков составляющих звеньев. Подставив значения получим: +50 = 0 – (-31) – С3 Þ С3 = -19 мкм; ВD = СD + ТD/2 = -19 + 18 = -1 мкм; НD = СD + ТD/2 = -19 – 18 = -37 мкм. Данные расчетов для удобства сведем в табл. 10. Для проверки правильности выбора допусков рассчитаем поле допуска замыкающего звена с заданной вероятностью:
Т а б л и ц а 10
|
- относительное среднеквадратическое отклонение, характеризующее закон распределения; wj – зона предельного рассеивания случайной величины. В случае нормального закона lj2 = 1/9, в случае закона Симпсона lj2 = 1/6, в случае закона равной вероятности lj2 = 1/3.
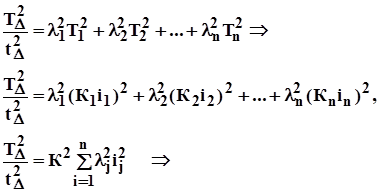
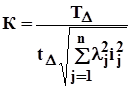. (6)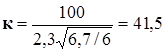
(к = 40 соответствует 9-му квалитету, а к = 64 соответствует 10-му квалитету). Выбираем ближайший 9 квалитет для всех звеньев.
(7)
< 100 мкм.
