Электромагнитные волны в двухпроводной линии конечной длины.
Описанные распространяющиеся электромагнитные волны возни
кают в очень длинных линиях, которые можно практически рассматривать как неограниченные (бесконечные). На практике обычно имеют дело с линиями, на протяжении которых укладывается сравнительно небольшое число длин волн. В этих случаях существенную роль играет отражение электромагнитных волн на концах лиши. Отраженные волны, складываясь с издающей волной, создают более сложные формы электромагнитных колебаний — стоячие электромагнитные волны, подобные стоячим механическим волнам в упругом шнуре или струне. В бегущей волне, как уже упоминалось, колебания электрического и магнитного полей происходят в одинаковых фазах (см. уравнение (2)). При отражении электромагнитной волны в конце линии происходит изменение фазы колебаний. Так как в бегущей волне.направления векторов v, E и Н связаны правилом правого винта, то в первичной волне, движущейся от генератора в положительном (Направлении оси X, расположение векторов v, Е, Н будет вблизи конца линии таким, как «а рис. 3, а. Чтобы направление распространения волны изменилось на противоположное, необходимо, чтобы один из векторов Е или Н изменил свое направление на противоположное (рис. 3,6 и 3,0). Но изменение направления поля означает изменение фазы колебаний на p. Поэтому при отражении, если меняется фаза электрического поля, фаза магнитного поля сохраняется и, наоборот, при изменении фазы магнитного поля фаза электрического поля остается неизменной. Это изменение фазы одной из составляющих электромагнитного поля следует из строгого рассмотрения отражений на основе уравнений Максвелла. При рассмотрении отражения электромагнитных волн от нагрузки линии вводят коэффициенты отражения по напряжению р£ и току ря [3]:
где
Рассмотрим режимы работы линии при некоторых сопротивлениях нагрузки. 1. Линия на конце разомкнута. Z,, = ¥;. Коэффициенты отражения Переменные токи, возникающие в линии, на конце ее будут вызывать наибольшие колебания зарядов. Так как проводимость между проводами идеальной линии отсутствует, то амплитуда тока проводимости на конце' линии равн Для отыскания распределения электромагнитного поля в двухпроводной линии при наличии отражений на разомкнутом конце запишем уравнения падающей и отраженной волн:
Результирующее электрическое поле
Результирующее магнитное поле
Формулы (7) и (8) показывают, что в линии будут происходить гармонические колебания с частотой 8. Координаты пучностей электрического поля находим из условия:
Из выражения (9) видно, что две соседние пучности электрического поля отстоят друг от друга на расстояние, равное λ/2. Координаты узлов электрического поля находим из условия: kxy£ = (2л + 1) Отсюда координаты узлов Е хуе = Расстояние между двумя соседними узлами электрического поля также составляет λ /2
. Из сравнения формул (9) и (10) видно, что между двумя соседними пучностями располагается один узел; между двумя соседними узлами располагается одна пучность. Из формулы (8) найдем координаты узлов и пучностей магнитного доля. Координаты узлов H находим из условия
Ъ
Из условия •находим координаты пучностей Н:
Из формул (11) и (12) видно, что для магнитного поля, так же, как и для электрического, расстояние между двумя соседними узлами и пучностями составляет . 2. Линия на конце короткозамкнута ZH = 0. Коэффициенты отражения В этом случае напряжение на конце линии будет всегда равно нулю, т. е. электрическое поле там будет отсутствовать. В замыкателе будет наибольшая амплитуда тока, и на конце линии — наибольшее магнитное поле. Для отыскания распределения поля в короткозамкнутой линии аналогично предыдущему случаю, запишем уравнения падающей и отраженной волн:
Епад = Е0 sin(ωt-kx) E отр = Е:пад ρЕ = -Е0 sin(ωt+kx) Нпад = Н0 Sin(ωt-kx) Hотр = Нпад ρн sin(ωt+kx)
Результирующее электрическое поле
Результирующее магнитное поле
Из условия
находим координаты узлов электрического поля
Из условия
находим координаты пучностей электрического поля:
Из условия
Из условия
kxnH='nrc, я = О, 1, 2,...
находим координаты пучностей магнитного поля:
ха„=пЦ2. (18) Полученные по уравнениям результаты можно представить з виде табл. 1.
Таблица 1
3. Линия замкнута на волновое сопротивление ZH = линии, нагруженной на волновое сопротивление
|

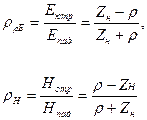 (5)
(5)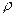 — волновое сопротивление линии;
— волновое сопротивление линии; 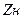 — сопротивление нагрузки, включенной на конце линии; в общем случае может быть комплексным.
— сопротивление нагрузки, включенной на конце линии; в общем случае может быть комплексным. = — 1;
= — 1; 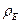 = 1.
= 1. а нулю, следовательно равно нулю магнитное поле, а электрическое поле максимальное.
а нулю, следовательно равно нулю магнитное поле, а электрическое поле максимальное.
 (7)
(7) (8)
(8) . Амплитуда колебаний электрического поля Е = 2E
. Амплитуда колебаний электрического поля Е = 2E  0coskx и магнитного поля Н — 2 Hosinkx - оказываются зависимыми от координаты, которая здесь отсчитывается от конца линии, и поэтому различны в разных точках линии. В определенных точках Е (или Н) достигает максимума. Эти точки называются пучностями электрического (или магнитного) поля. В точках, называемых узлами электрического (или магнитного) поля, амплитуда Е (соответственно, Н) обращается в нуль
0coskx и магнитного поля Н — 2 Hosinkx - оказываются зависимыми от координаты, которая здесь отсчитывается от конца линии, и поэтому различны в разных точках линии. В определенных точках Е (или Н) достигает максимума. Эти точки называются пучностями электрического (или магнитного) поля. В точках, называемых узлами электрического (или магнитного) поля, амплитуда Е (соответственно, Н) обращается в нуль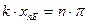 (где п =0, 1, 2....). Отсюда координаты пучностей Е
(где п =0, 1, 2....). Отсюда координаты пучностей Е (9)
(9)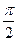 , где п = О, 1, 2,...
, где п = О, 1, 2,... (10)
(10) , где л = О, 1, 2,... Отсюда координаты узлов H
, где л = О, 1, 2,... Отсюда координаты узлов H (11)
(11)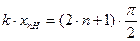
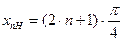 (12)
(12)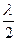 . Между двумя соседними пучностями располагается один узел; между двумя соседними узлами располагается пучность. Отличие в распределении электрического и магнитного полей в стоячей электромагнитной волне состоит в том, что узлу электрического поля соответствует пучность магнитного поля и наоборот
. Между двумя соседними пучностями располагается один узел; между двумя соседними узлами располагается пучность. Отличие в распределении электрического и магнитного полей в стоячей электромагнитной волне состоит в том, что узлу электрического поля соответствует пучность магнитного поля и наоборот
 (13)
(13) (14)
(14) , где
, где 

 ; n = 0, 1,2,...
; n = 0, 1,2,... (16)
(16)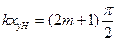
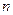 = 0, 1, 2,... (17)
= 0, 1, 2,... (17)
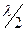
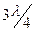

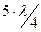
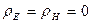 . Распространяющаяся от генератора волна будет полностью поглощаться в нагрузке, и отраженной волны не будет. В короткой
. Распространяющаяся от генератора волна будет полностью поглощаться в нагрузке, и отраженной волны не будет. В короткой


