Некоторые типы иррациональных уравнений
Пусть далее I тип: уравнение вида
Возведение в Уравнение
после возведения в Уравнение
после возведения в степень 2 n приводит к уравнению-следствию
Найденные корни уравнения (5.4) проверяют подстановкой в уравнение (5.3) и отбирают те из них, которые удовлетворяют уравнению (5.3). Уравнение
после возведения в степень 2 n сводится к уравнению-следствию
Корни уравнения (5.6) необходимо проверить подстановкой в уравнение (5.5). II тип: уравнение вида
где 1-й способ. Необходимо возвести уравнение (5.7) в квадрат. В определенных случаях следует один из корней перенести в правую часть уравнения. После упрощения полученное уравнение возводят в квадрат еще раз. 2-й способ. Умножение уравнения (5.7) на сопряженное выражение
Отдельно проверяют, имеет ли решение уравнение h (x) = 0. Затем для h (x) ¹ 0 рассматривают систему
Сложение уравнений этой системы приводит к уравнению вида (5.3). 3-й способ. Замена переменных
и переход к системе уравнений относительно u, v. Уравнение
где a, b Î R, возведением в куб обеих частей сводится к уравнению
Выражение в скобках (в левой части уравнения (5.9)) заменяют на Полученные таким образом решения необходимо проверить подстановкой в уравнение (5.8). III тип: уравнения, решаемые заменой переменной. В результате замены может уменьшиться степень выражений, стоящих под корнями, что приведет к уменьшению степени рационального уравнения после избавления от корней. Если уравнение имеет вид
где F – некоторое алгебраическое выражение относительно
После решения уравнения (5.11) возвращаются к старой переменной и находят решения уравнения (5.10). IV тип: уравнения, решаемые исходя из арифметического смысла корней с четными показателями. В частности, решение уравнения
где a > 0, b > 0, сводится к решению системы
V тип: уравнения, решаемые функциональными методами и методами, основанными на ограниченности входящих в уравнение функций. Решение уравнений основывается на следующих утверждениях. 1. Если
2. Если функции f (x) и g (x) непрерывны и f (x) возрастает, а g (x) убывает для x Î X, то уравнение f (x) = g (x) имеет не больше одного решения на промежутке X. Если один корень подобрать, то других корней нет. 3. Если f (x) – возрастающая функция, то уравнение 4. Если f (x) – возрастающая (убывающая) функция, то уравнение
Пример 1. Решить уравнение Решение. Возведем обе части уравнения в квадрат:
Приводим подобные. При этом в левой части уравнения записываем корень, остальные слагаемые – в правой части:
Возводим полученное уравнение в квадрат еще раз:
Решая последнее квадратное уравнение, находим корни Приходим к ответу: Пример 2. Решить уравнение Решение. Возведем обе части уравнения в куб:
Воспользовавшись исходным уравнением, заменим выражение
Решаем совокупность уравнений
В результате замены выражения могут появиться посторонние корни, так как такое преобразование не является равносильным. Поэтому необходимо произвести проверку. Подставляем найденные значения и убеждаемся, что они являются корнями исходного уравнения. Приходим к ответу:
Пример 3. Решить уравнение Решение. Возведение уравнения в квадрат приводит к уравнению четвертой степени и громоздкому решению. Нетрудно заметить, что в данном уравнении можно произвести замену. Но перед этим преобразуем уравнение следующим образом:
Заменив
Решая его, находим корни Возвращаемся к исходной неизвестной:
Первое уравнение решений не имеет, так как его левая часть неотрицательна, а правая – отрицательна. Второе уравнение возводим в квадрат. Получаем:
Его корни
Пример 4. Решить уравнение Решение. 1-й способ. Перенесем второй корень вправо:
Возводим обе части в квадрат:
Еще раз возводим в квадрат и получаем квадратное уравнение, решая которое и получаем корни 2-й способ. Введем замену
Возведем его в квадрат:
Возвращаемся к исходной неизвестной:
Возводим обе части уравнения в квадрат:
При помощи проверки убеждаемся, что оба корня подходят. 3-й способ. Домножим обе части уравнения на выражение, сопряженное левой части исходного уравнения. Получим:
Сложим последнее уравнение с исходным. Получим:
Последнее уравнение возводим в квадрат. Получаем квадратное уравнение
Решая его, находим корни Приходим к ответу: Пример 5. Решить уравнение Решение. Пусть Получили систему
Решаем ее методом подстановки:
Второе уравнение решим отдельно
Получаем корни:
Возвращаемся к системе:
Получаем:
Переходим к заданным неизвестным:
Решая последнюю совокупность, находим корни Получили ответ: При решении иррациональных уравнений, как правило, нахождение ОДЗ является бесполезным, так как проверка решений по ОДЗ недостаточна. Но существует ряд примеров, в которых нахождение ОДЗ является тем методом, который приводит к успеху. Покажем это на следующем примере.
Пример 6. Решить уравнение
Решение. Найдем ОДЗ данного уравнения:
Решаем последнюю систему неравенств графически (рис. 5.10).
Рис. 5.10
Получили, что ОДЗ состоит из единственной точки Остается подставить значение
Получили, что
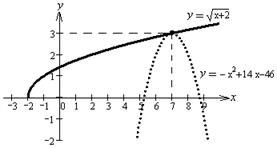
Пример 7. Решить уравнение Решение. Используем графический способ. Строим графики функций
Рис. 5.11
Из рисунка видно, что графики пересекаются в единственной точке x = 7. Следовательно, уравнение имеет единственное решение. Проверяем x = 7 подстановкой в заданное уравнение и убеждаемся, что это точное значение решения уравнения. Получили ответ: x = 7.
|

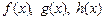 – некоторые выражения с неизвестной х,
– некоторые выражения с неизвестной х, 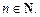
 (5.1)
(5.1)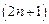 -ю степень приводит к равносильному уравнению
-ю степень приводит к равносильному уравнению 
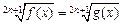 (5.2)
(5.2)
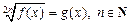 (5.3)
(5.3) (5.4)
(5.4) (5.5)
(5.5) (5.7)
(5.7)

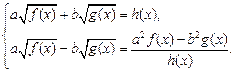

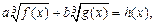 (5.8)
(5.8)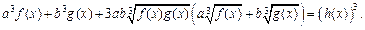 (5.9)
(5.9)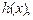 используя заданное уравнение. В итоге заданное уравнение (5.8) приводится к уравнению-следствию, которое снова возводят в куб.
используя заданное уравнение. В итоге заданное уравнение (5.8) приводится к уравнению-следствию, которое снова возводят в куб.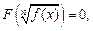
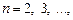 (5.10)
(5.10)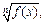 то заменой
то заменой  оно сводится к уравнению
оно сводится к уравнению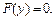 (5.11)
(5.11) (5.12)
(5.12)
 и
и 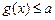 для всех
для всех 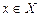 , то на множестве X уравнение f(x) = g(x) равносильно системе уравнений
, то на множестве X уравнение f(x) = g(x) равносильно системе уравнений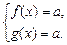
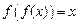 равносильно уравнению
равносильно уравнению 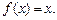
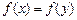 равносильно уравнению
равносильно уравнению 





 которые теперь необходимо проверить. Делаем проверку корней подстановкой в исходное уравнение. Первый корень не подходит.
которые теперь необходимо проверить. Делаем проверку корней подстановкой в исходное уравнение. Первый корень не подходит.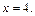


 выражением
выражением 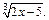 Получаем:
Получаем:
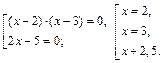

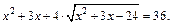
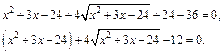
 получаем квадратное уравнение
получаем квадратное уравнение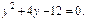

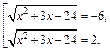
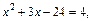 т. е.
т. е. 
 С помощью проверки убеждаемся, что оба корня подходят, т. е. приходим к ответу:
С помощью проверки убеждаемся, что оба корня подходят, т. е. приходим к ответу: 


 Делаем проверку корней подстановкой в исходное уравнение. Оба корня подходят.
Делаем проверку корней подстановкой в исходное уравнение. Оба корня подходят. тогда
тогда 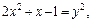
 Таким образом получили более простое уравнение
Таким образом получили более простое уравнение т. е.
т. е. 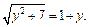


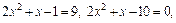 откуда
откуда 
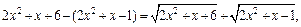

 т. е.
т. е. 



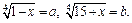 Тогда
Тогда  и
и 
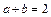 по условию.
по условию.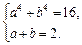

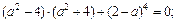

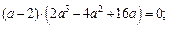
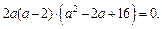
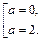



 и
и 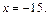 С помощью проверки убеждаемся, что оба корня подходят.
С помощью проверки убеждаемся, что оба корня подходят.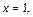


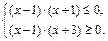





 (рис. 5.11).
(рис. 5.11).