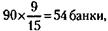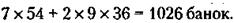РЕШЕНИЯ 2 страница
По условиям задачи это равенство должно иметь место для любой пары, поэтому с учетом
а также
Поскольку для последней пары, где Чn = 0, Нn = 6 - 0 = 6, а для первой пары Н1 может быть минимально равно 0, при этом Ч1 = 6 - 0 = 6. По условиям задачи от пары к паре количество производственных помещений для нечетных предприятий увеличивается на единицу, в распределении может участвовать всего 7 пар (имеющих Нn от 0 до 6, включая 0), т. е. 7 х 2 = = 14 малых предприятий. При этом в соответствии с (*):
Итак: 1) Ресурсы могут распределяться между 14 малыми предприятиями. 2) Всего распределяется 42 производственных помещения. Торговых точек для уравнивания возможностей МП должно быть столько, чтобы у каждого предприятия было по 6 единиц ресурсов, т. е. каждая пара предприятий должна получить по 6 торговых точек, а всего 6 x 7 пар предприятий = 42 торговые точки. 3) Количество ресурсов обоих видов, полученных каждым предприятием, будет следующим:
30. Оказывается, это довольно просто. Дело в том, что, к счастью аудитора, суммы цифр в обоих слагаемых оказались кратны 9, а значит – слагаемые делятся на 9. Естественно, делились на 9 они и до перестановки в них цифр. При сложении же чисел, делящихся на 9, сумма также делится на 9. Это означает, что сумма цифр результата сложения должна быть кратна 9. Сложив цифры суммы (кроме подделанной), получим 30. Ближайшее большее число, кратное 9, это 36. Нам не хватает 36 - 30 = 6. Следовательно, исправленная цифра – это 6. 31. Обозначим через х площадь арендуемого фирмой помещения, а через у – количество единиц продукции, идущих в уплату аренды. Тогда условие задачи можно записать так:
32. Обозначим через т, п, р, q количество контейнеров, поставляемых фирмами первой четверки (не обязательно в порядке последовательности фирм), которые являются партнерами соответствующих (в порядке номеров) фирм второй четверки (т - поставка партнера фирмы № 5, п - фирмы № 6 и т. д.). При этом условие задачи можно записать так:
(44 –это разность общего количества контейнеров и 20 – числа контейнеров, поставляемых первой четверкой: 2 + 4 + 6 + 8 = 20).
Умножая обе части (2) на 2, получим:
Из последнего выражения следует, что q может быть равно только 4, ибо по условиям задачи: 1) q, m,p должны быть целыми положительными числами, 2) эти числа различны и могут быть только 2, 4, 6, 8, 3) 2 не подходит, так как при этом т = р, 4) 6 и 8 не подходят, так как при этом т - р>8. Итак, q = 4. Тогда из (*) следует, что 2(4-2) = m-р, т- р = 4. Последняя разность может иметь место лишь при следующих значениях пары т и р:
Первая пара не подходит, так как число 4 уже имеет «хозяина» – ему равно q. Следовательно, т = 6р = 2. Для п остается лишь значение, равное 8.
Если выстроить значение этих показателей по ранжиру (р, q, т, п), то эта последовательность и будет соответствовать последовательности номеров фирм-партнеров из второй четверки фирмам первой четверки (где была последовательность т, п, р, q): фирма № 5 является партнером фирмы № 3, фирма № 6 является партнером фирмы № 4, фирма № 7 является партнером фирмы № 1, фирма № 8 является партнером фирмы № 2. Подставляя соответствующие значения в (1), нетрудно рассчитать количество контейнеров, поставляемых фирмами второй четверки. Итоговые данные по поставкам всеми фирмами будут следующими:
33. Обозначим начальные фонды, равные у обоих предприятий, через х. Тогда к моменту окончания первой операции предприятие А обладало фондом в размере, равном х + 30, а предприятие Б – х - 30 тыс. у. д. ед. К моменту окончания второй операции фонд предприятия А составлял:
34. Взнос предпринимателя В, равный 320 тыс. у. д. ед., составляет Теперь нужно разделить сумму, равную взносу В, между А и Б так, чтобы у каждого из них оказалось по 35. Обозначим через длину отрезка проволоки, причитающейся владельцу Б. Тогда условие задачи можно будет записать так:
Решая это уравнение, получим:
Владельцу А будет причитаться:
36. Обозначим через х стоимость месячного содержания помещений. Тогда условие задачи можно записать так:
Откуда, после преобразований, х = 150 тыс. у. д. ед. Вычитая полученную стоимость содержания помещений из дохода, получим величину ежемесячных потерь арендатора:
37. Обозначим через х количество участков для субаренды. Тогда выручка за субаренду составит 8х, годовой заработок будет равен
и условие задачи запишется так:
После преобразований получим:
Решая квадратное уравнение по стандартной формуле, получим:
Следовательно: 1) Количество участков равно 12. 2) Прибыль арендатора равна:
38. Обозначим через Ст, Ср и Мл обобщенных представителей старших, средних и младших владельцев каждой группы. Тогда по условиям задачи:
Это равнозначно следующим обозначениям:
так как, подставляя значения из (2) в (1), получаем тождество:
Далее, вводя новые обозначения, можно показать, что имеют место следующие равенства:
так как, подставляя значения из (3) в (2), получаем тождество:
Обозначим
Тогда с учетом (2) и (3) можно записать:
Подбираем значения m и n исходя из следующих условий: – т > п (иначе z будет отрицательным или равным 0, что противоречит условиям задачи); – т и п должны быть целыми положительными числами разной четности (разная четность т и n объясняется так: 1) из Ср2 = х2 + у2 следует разная четность х и у – сторон прямоугольного треугольника; 2) поскольку у = 2ху в любом случае четен, х должен быть нечетным; 3) чтобы х был нечетным, необходимо, чтобы тип,связанные с х зависимостью х = т2 - п2, были разной четности); – т и п должны удовлетворять условию х1 + у1 = Ср2 (из х2 + у2 должен без остатка извлекаться квадратный корень):
Наименьшей возможной парой т и п, удовлетворяющей всем этим условиям, является пара 8 и 7. При этом
Поскольку по условиям задачи минимальная доля (2 тыс. у. д. ед.) принадлежит младшему афганцу, ему причитается и наименьшая премия, равная 2'2 = 4 тыс. у. д. ед. Откуда премия среднего афганца равна:
а старшего афганца –
Соответственно их доли составляют:
Доля средней сестры равна:
а ее премия –
Премия младшей сестры равна:
а старшей–
Соответственно их доли составляют:
Доля старшего брата равна:
127 - 33 = 94 тыс. у. д. ед.,
а его премия – 942 = 8836 тыс. у. д. ед. Премия среднего брата равна:
8836 - 3360 = 5476 тыс. у. д. ед, а младшего брата –
5476 - 3360 = 2116 тыс. у. д. ед.
Соответственно их доли составляют:
39. Обозначим общее количество отечественных и иностранных фирм через х (при этом х должен быть целым, положительным и четным числом). Тогда каждая фирма должна израсходовать
При этом х может быть 2, 4, 6... С учетом того, что конструкция А стоит 1 тыс. у. д. ед., конструкция Б – х = 2 отпадает, так как речь идет о ряде как отечественных, так и иностранных фирм; х = 4 также не проходит, так как при этом каждая фирма способна тратить при х = 6 расходы каждой фирмы составили
Это и будет ответом на первый вопрос. Общее количество фирм, участвующих в покупке, равно 6 (3 отечественные и 3 иностранные). 40. Обозначая момент проверки постов охраны через х1 можно математически записать условие задачи так:
Решая это уравнение, получим:
41. Вероятность получения счастливого билета (Р) может быть определена по следующей формуле из теории вероятностей:
Этот расчет можно проверить, собрав достаточное количество (порядка тысячи) любых билетов с шестизначными номерами и сосчитав, сколько счастливых приходится в среднем на сотню. Должно получиться 5–6 билетов. 42. 1) Обозначим через О, М и Д возраст отца, матери и дочери в момент заключения страхового договора. При этом условие задачи математически запишется так:
в момент заключения договора,
в момент заключения договора,
в момент выплаты страховой премии (через М лет). Из (2) следует, что О = 12Д. Подставляя значение О в (3), получим:
Подставляя значение О и М в (1), получим: 12Д + 10Д + Д = 46, откуда Д - 2 года, О = 12Д = 24 года, М = 10Д = 20 лет. 2) Страховая премия должна быть выплачена через М = 20 лет после заключения договора.
43. Обозначим через х первоначальное количество работников в каждом малом предприятии, а через у – первоначальное количество этих предприятий. Тогда количество предприятий после первой реорганизации будет у -10, а количество работников в каждом из них х + 1. После второй реорганизации получим соответственно у – 10 - 15 = у - 25 предприятий и х+ 1 + 2 = х + 3работника в каждом. При данном условии задачи можно записать так:
Из (1) следует:
Совместно решая (1) и (2), получим:
Подставляя (*) в (**), получим:
Общая численность работников объединения равна:
44. Обозначим время от полудня до противостояния стрелок через х, а число делений, проходимых часовой стрелкой от цифры 12 до момента противостояния, – через у. Тогда условие задачи можно записать следующим образом:
где
1) Следовательно, заседание должно начаться в 12 ч 32 мин 43,6 с. 2) Следующее противостояние должно произойти через 2х часов, т. е. через
45. Проанализируем ситуацию с помощью графика (см. рис.). По оси х откладывается время возможного прихода партнера А, а по оси у – партнера Б. Тогда время, в течение которого они могут встретиться, будет соответствовать заштрихованному участку графика. Действительно, если партнер А придет на встречу в начале срока (точка 0), то его встреча с партнером Б состоится, лишь если Б придет на встречу в пределах от 0 до 20 мин от начала срока. Если он придет позже, встреча не состоится, так как А уже уйдет. Если же А придет на встречу на 40-й мин, то он встретится с Б, лишь если тот придет между 20-й и 60-й мин. И так для всех точек заштрихованной области.
Вероятность встречи может быть найдена как отношение шансов, благоприятствующих встрече (заштрихованная область), ко всем возможным шансам (площадь квадрата со стороной в 60 мин). При этом, как видно из рисунка, площадь, соответствующая всем возможным шансам, равна:
а площадь, соответствующая благоприятным шансам, равна разности полученной площади и двух треугольников:
Следовательно, искомая вероятность встречи равна:
Иными словами, встреча состоится 5–6 раз из 10. 46. Обозначим новые оклады работников начальными буквами соответствующих специальностей. Тогда условие задачи можно будет записать так:
Группируя оклады, получим:
Поскольку Р + М = 2500, выражение (*) можно представить так:
откуда
И далее:
1) Учитывая, что эти оклады составляют 100 - 25 = 75 % от соответствующих окладов до сокращения, несложно рассчитать, чему были равны тогда упомянутые оклады (пометим их штрихами):
Расходы на зарплату составляли удвоенную сумму этих окладов:
2) Следовательно, экономия средств, полученная предприятием за счет сокращения, равна:
14400-11 300 = 3100 у. д. ед. в месяц. 47. Обозначив через х количество персонала на предприятии до реорганизации, а через у – количество дней, на которые хватает при этом зарплаты, запишем условие задачи следующим образом:
Решая это уравнение относительно второго и третьего равенств, получим:
180 у = 15 х - 600, откуда
Из (*) следует также, что
Подставляя в последнее выражение значение у, получим:
откуда х = 400 человек, у = 30 дней. Следовательно: 1) В настоящее время на предприятии работает 400 человек. 2) Величина месячной (30-дневной) зарплаты составляет:
48. Вначале определим количество участков, на которые увеличится садоводство:
Обозначим через х сторону садоводства до его увеличения, выраженную в длинах сторон участков. Тогда площадь садоводства до увеличения составит х2, а после увеличения (x + n)2, где п = 1, 2, 3, 4, 5... (целые числа натурального ряда, соответствующие приросту длины садоводства, выраженной в длинах сторон участков). Теперь условие задачи можно записать так:
Откуда
Анализ последнего выражения и условий задачи показывает, что x2 и п должны быть целыми числами, а п, кроме того, должно быть нечетным (иначе 161 не разделится на него без остатка) и на него должно делится без остатка 161. Этим условиям из первых 10 цифр натурального ряда отвечают только 1 и 7. Но 7 не подходит, так как в этом случае х = 7 = п и из выражения (*) следует, что
Итак, п = 1. Это означает, что
Следовательно: 1) Количество участков в садоводстве до его увеличения было
а после увеличения:
или, что то же самое, 6400 + 161 = 6561 участок. 2) Сторона садоводства при увеличении должна вырасти на длину одного участка (n = 1), т. е. на
3) Площадь садоводства до увеличения была равна:
а после увеличения:
49. Обозначим через х количество работников, а через у – их зарплату при работе предприятия в нормальном режиме. Тогда условие задачи можно записать так:
Из второго равенства уравнения (*) следует:
Из первого равенства уравнения (*) следует:
Подставляя в последнее выражение значение х, получим:
Итак: 1) Численность персонала при работе в нормальном режиме составляет 40 человек; зарплата при этом равна 9 тыс. у. д. ед. 2) Фонд заработной платы равен 40 х 9 = 360 тыс. у. д. ед. 3) Численность персонала при работе в период спада равна 40 - 10 = 30 человек, а зарплата 9 + 3 = 12 тыс. у. д. ед.; численность персонала при работе в период увеличения загрузки равна 40 + 50 = 90 человек, а зарплата 9-5 = 4 тыс. у. д. ед.
50. 1) Исходя из того, что 6 путевок в Каркодайл равноценны 9 путевкам в Фингалию, определим относительную ценность этих путевок.
Она составит
2) Исходя из этих относительных стоимостей и зная, что поездка в Каркодайл и в Фингалию в сумме оценивается в 90 банок икры, рассчитаем стоимость каждой из путевок в отдельности:
путевка в Каркодайл стоит путевка в Фингалию
3) Информация о двух возможных вариантах приобретаемого количества путевок позволяет составить систему из двух уравнений с двумя неизвестными:
где К и Ф – количество путевок в Каркодайл и Фингалию соответственно. Решение этой системы уравнений позволяет найти К = 7 и Ф = 9. 4) Подставляя эти цифры в уравнение, соответствующее второму варианту сделки, можно получить искомое количество банок икры, выделенных для этой сделки:
51. 1) В исходном положении сосуд № 1 содержит 1,1л тоника, а сосуд № 2 – 0,5 л джина. 2) Из сосуда № 1 в сосуд № 2 переливается 0,5 л тоника (чтобы удвоить там количество жидкости). Теперь в сосуде № 1 осталось 0,6 л тоника, а в сосуде № 2 оказался 1 л смеси, состоящей поровну из джина и тоника. 3) Из сосуда № 2 в сосуд № 1 переливается 0,6 л (столько, сколько оставалось в сосуде № 1) смеси, состоящей из 0,3 л джина и 0,3 л тоника. Теперь в сосуде № 1 0,3 л джина и 0,9 л тоника, а в сосуде № 2 осталось 0,2 л джина и 0,2 л тоника. 4) Из сосуда № 1 в сосуд № 2 переливается 0,4 л (чтобы удвоить там количество) смеси, содержащей 0,1 л джина и 0,3 л тоника (смесь в сосуде № 1 имеет соотношение джина и тоника 1: 3). После всего этого количество жидкости в сосудах становится по 0,8 л. В сосуде № 1 образовалась смесь из 0,6 л джина и 0,2 л тоника (3: 1 – крепкий коктейль).
|


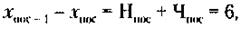





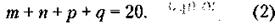





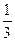 прежнего складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5: 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.
прежнего складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5: 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.



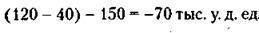
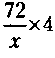
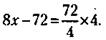
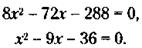
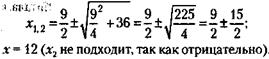
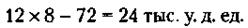

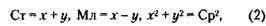
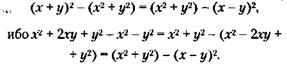
 (3)
(3)




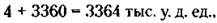


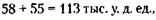
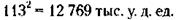


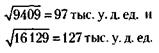
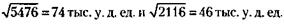

 а конструкция В –
а конструкция В – 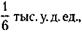 будем рассуждать так:
будем рассуждать так: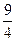 тыс. у. д. ед. и не может на эти деньги купить целое число конструкций всех видов;
тыс. у. д. ед. и не может на эти деньги купить целое число конструкций всех видов; На эти деньги можно купить по одной конструкции вида А, по одной конструкции вида Б и по одной – вида В:
На эти деньги можно купить по одной конструкции вида А, по одной конструкции вида Б и по одной – вида В:
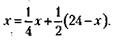



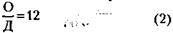

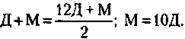




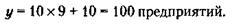
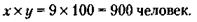
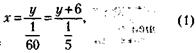
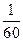 – скорость минутной, а
– скорость минутной, а 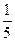 – скорость часовой стрелки.
– скорость часовой стрелки.
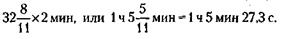






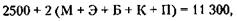





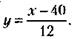

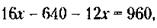
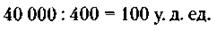
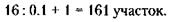

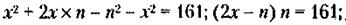
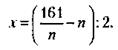
 – не целое число.
– не целое число.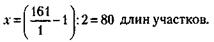

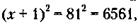
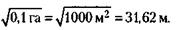


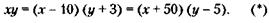
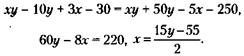



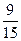 для Каркодайла и
для Каркодайла и  для Фингалии.
для Фингалии.