В метрологии под модуляцией понимается процесс, при котором измерительный сигнал 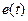 воздействует на какой-либо параметр некоторого стационарного сигнала
воздействует на какой-либо параметр некоторого стационарного сигнала 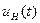 , обладающего такой физической природой и таким характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала именуемого несущим, обычно выбирают либо последовательность импульсов, либо синусоидальное (гармоническое) колебание:
, обладающего такой физической природой и таким характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала именуемого несущим, обычно выбирают либо последовательность импульсов, либо синусоидальное (гармоническое) колебание:

где  - амплитуда в отсутствии модуляции;
- амплитуда в отсутствии модуляции;
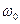 - угловая (круговая) частота;
- угловая (круговая) частота;
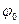 - начальная фаза;
- начальная фаза;
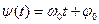 - полная фаза.
- полная фаза.
В зависимости от того, какой из параметров гармонического несущего колебания подвергается воздействию, различают амплитудную, частотную, фазовую и ряд видов импульсной модуляции.
Физический процесс, обратный модуляции, называется демодуляции или детектированием, и заключается в получении из модулированного колебания сигнала, пропорционального модулирующему.
Наиболее простым модулированным сигналом является амплитудно-модулированный сигнал, в котором измерительная информация заложена в амплитуду 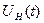 несущего колебания
несущего колебания 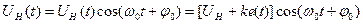 , где
, где  - безразмерный коэффициент пропорциональности.
- безразмерный коэффициент пропорциональности.
Пусть модулирующий сигнал – гармоническое колебание вида  . Тогда, приняв для упрощения
. Тогда, приняв для упрощения 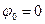 , и подставив в формулу для колебания этот сигнал, получим:
, и подставив в формулу для колебания этот сигнал, получим: 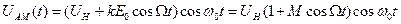 , где
, где 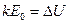 –максимальное отклонение амплитуды АМ – сигнала от амплитуды несущей
–максимальное отклонение амплитуды АМ – сигнала от амплитуды несущей  ;
;  – коэффициент или глубина амплитудной модуляции.
– коэффициент или глубина амплитудной модуляции.
Сигналы с частотной модуляцией.
При частотной модуляции несущая частота 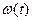 связана с модулирующим сигналом
связана с модулирующим сигналом 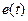 зависимостью:
зависимостью: 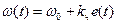 , где
, где  - размерный коэффициент пропорциональности.
- размерный коэффициент пропорциональности.
Рассмотрим однотональную частотную модуляцию, когда модулирующим колебанием является гармоническое колебание  . Тогда, приняв для упрощения
. Тогда, приняв для упрощения 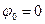 , определим полную фазу ЧМ сигнала в любой момент времени
, определим полную фазу ЧМ сигнала в любой момент времени  путем интегрирования частоты, выраженной
путем интегрирования частоты, выраженной 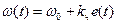 :
:

где 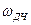 =
= 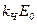 - максимальное отклонение частоты от значения
- максимальное отклонение частоты от значения 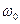 или девиация частоты при частотной модуляции.
или девиация частоты при частотной модуляции.
Отношение  , являющееся девиацией фазы несущего колебания, называют индексом частотной модуляции.
, являющееся девиацией фазы несущего колебания, называют индексом частотной модуляции.
С учетом этого выражения ЧМ сигнал запишется как
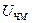 =
= 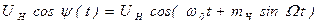 .
.

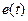 воздействует на какой-либо параметр некоторого стационарного сигнала
воздействует на какой-либо параметр некоторого стационарного сигнала 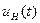 , обладающего такой физической природой и таким характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала именуемого несущим, обычно выбирают либо последовательность импульсов, либо синусоидальное (гармоническое) колебание:
, обладающего такой физической природой и таким характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала именуемого несущим, обычно выбирают либо последовательность импульсов, либо синусоидальное (гармоническое) колебание:
 - амплитуда в отсутствии модуляции;
- амплитуда в отсутствии модуляции;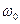 - угловая (круговая) частота;
- угловая (круговая) частота;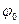 - начальная фаза;
- начальная фаза;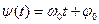 - полная фаза.
- полная фаза.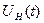 несущего колебания
несущего колебания 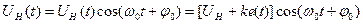 , где
, где 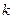 - безразмерный коэффициент пропорциональности.
- безразмерный коэффициент пропорциональности. . Тогда, приняв для упрощения
. Тогда, приняв для упрощения 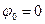 , и подставив в формулу для колебания этот сигнал, получим:
, и подставив в формулу для колебания этот сигнал, получим: 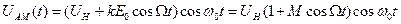 , где
, где 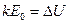 –максимальное отклонение амплитуды АМ – сигнала от амплитуды несущей
–максимальное отклонение амплитуды АМ – сигнала от амплитуды несущей  – коэффициент или глубина амплитудной модуляции.
– коэффициент или глубина амплитудной модуляции.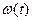 связана с модулирующим сигналом
связана с модулирующим сигналом 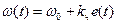 , где
, где  - размерный коэффициент пропорциональности.
- размерный коэффициент пропорциональности. . Тогда, приняв для упрощения
. Тогда, приняв для упрощения 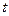 путем интегрирования частоты, выраженной
путем интегрирования частоты, выраженной 
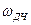 =
= 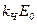 - максимальное отклонение частоты от значения
- максимальное отклонение частоты от значения  , являющееся девиацией фазы несущего колебания, называют индексом частотной модуляции.
, являющееся девиацией фазы несущего колебания, называют индексом частотной модуляции.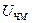 =
= 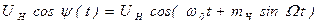 .
.


