Периодические и импульсные измерительные сигналыПериодические сигналы. Периодическим называют любой измерительный сигнал, повторяющийся через регулярные интервалы времени и удовлетворяющий условию: Периодическая последовательность импульсов описывается рядом:
где - амплитудой (высотой) - длительностью (шириной) - периодом следования - положением импульсов во времени относительно тактовых точек.
Одиночный прямоугольный импульс описывают уравнением:
т.е. он формируется как разность двух единичных функций
Последовательность прямоугольных импульсов представляет собой известную сумму одиночных импульсов:
Отношение периода к длительности прямоугольного импульса называется скважностью Представим периодический сигнал тригонометрической формы ряда Фурье:
В этом соотношении его составляющие принято называть: - постоянная составляющая Амплитуды косинусоидальных составляющих Амплитуды синусоидальных составляющих
Часто ряд Фурье удобнее представлять эквивалентной формой
Где Периодический сигнал обладает линейчатым (дискретным) спектром. Спектральную составляющую с частотой Наиболее наглядно о спектре сигнала можно судить по спектральной диаграмме. Различают амплитудно-частотные и фазочастотные спектры. Совокупность амплитуд гармонических составляющих На спектральных диаграммах по оси абсцисс откладывают текущую частоту, а по оси ординат – либо вещественную, либо комплексную амплитуду, или фазу соответствующих гармонических составляющих анализируемого сигнала. Спектр периодического сигнала принято называть линейчатым или дискретным, так как он состоит из отдельных линий, высота которых равна амплитуде соответствующих гармоник. Частота первой гармоники спектра сигнала равна частоте следования импульсов Непериодические (импульсные) сигналы. В практике измерений встречаются непериодические сигналы, отражающие физическую величину на небольшом интервале времени. Эти сигналы имеют сплошной спектр и описываются интегральными преобразованиями Фурье:
Эти соотношения называются соответственно прямым и обратным преобразованиями Фурье. Они связывают между собой вещественную функцию времени (сигнал)
|
, где 
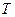- период повторения (следования) импульсов; n = 0,1, 2,...,....
,
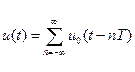- форма одиночного импульса, характеризующаяся следующим параметрами: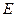
;
;
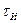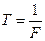, где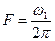 
- циклическая частота следования;
,
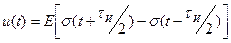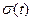(функций включения, или функций Хевисайда), сдвинутых во времени на 
.
.
.
;
;
.
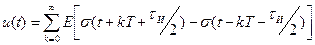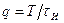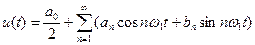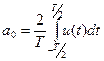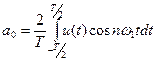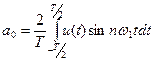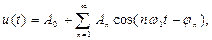
- амплитуда,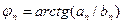 
- начальная фаза 
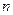-й гармоники сигнала.
в радиотехнике называют первой (основной) гармоникой, а составляющие с частотами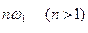 
- высшими гармониками периодического сигнала.
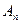носит название спектра амплитуд, а 
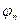- спектра фаз.
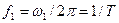. Частота второй – удвоенной частоте следования импульсов 
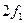и т.д. Амплитуды гармоник с увеличением их номера уменьшаются, поэтому считают, если полоса пропускания схемы лежит в пределах от 
до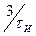 
, то она не вносит заметных искажений в передаваемый импульсный сигнал.
.
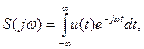
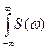
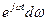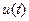и комплексную функцию частоты 
.
