Основные сведения об импульсной и цифровой технике измерений
Импульсное и цифровое представление информационных сигналов широко применяют в измерительной технике. При этом аналоговый сигнал, отражающий параметры реального физического процесса, преобразуется в последовательность импульсных сигналов, пригодных для обработки цифровыми устройствами. Напомним, что устройства, преобразующие аналоговый сигнал в импульсный (цифровой) вид, называются аналогово-цифровыми преобразователями (АЦП), а устройства обратного преобразования – цифроаналоговыми преобразователями (ЦАП). Исходной предпосылкой возможности построения цифровых измерительных приборов, и в частности АЦП и ЦАП, служит известная в радиотехнике теорема Котельникова (теорема отсчетов). Согласно одной, наиболее известной интерпретации теоремы Котельникова, произвольный сигнал При переходе от аналогового (непрерывного) сигнала к цифровому осуществляется три специфических преобразования: дискретизация по времени, квантование по уровню амплитуд и кодирование (оцифровка). Такое представление сигналов называют аналогово-цифровым преобразованием. Под дискретизацией по времени понимают процесс представления (замену) во времени аналогового сигнала последовательностью отсчетов (выборок), следующих с заданным временным интервалом Для представления дискретных отсчетов цифровыми сигналами (кодирования) их предварительно квантуют по уровню амплитуд. В процессе квантования весь диапазон возможных изменений амплитуд аналогового сигнала от 0 до
В цифровой технике для отражения измерительной информации используют кодовые слова. Как правило, информация (кодовые слова) представляется импульсными сигналами прямоугольной формы, имеющими два фиксированных уровня напряжения 1 и 0. таким образом, кодовое слов в цифровой технике имеет вид последовательности символов 1 и 0 определенной длины, например 01110101010. Теоретической базой построения систем цифровой обработки информации являются дискретная математика и алгебра логики Буля. В основе алгебры логики лежат несколько аксиом и законов, и три элементарные операции: ИЛИ (логическое сложение, или дизъюнкция), И (логическое умножение, или конъюнкция) и НЕ (логическое отрицание, или инверсия). Логический элемент ИЛИ имеет два или более входов и один выход. Операция дизъюнкции для n переменных имеет вид На выходе такого элемента при наличии хотя бы одного их слагаемых будет иметь место единичный уровень выходного напряжения. Обозначается такой элемент 1. Логический элемент И (логическая схема совпадения) содержит два или более входов и один выход. Операция конъюнкции для n переменных имеет вид На выходе такого элемента только при наличии всех сомножителей будет иметь место единичный уровень выходного напряжения, во всех остальных случаях – нулевой. Обозначается такой элемент & (and – читается «энд», т.е. И). Логический элемент НЕ (инвертор) выполняет функцию инверсии, т.е. инвертирует входную логическую величину в соответствии с формулой В условном обозначении элемента НЕ операция инверсии отражена кружком на выходе схемы. В измерительной технике часто встречаются комбинированные схемы обработки сигналов: ИЛИ – НЕ и И – НЕ:
|

 , спектр которого ограничен некоторой верхней частотой FВ, модет быть восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени
, спектр которого ограничен некоторой верхней частотой FВ, модет быть восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени  .
. , и по которым с заданной точностью можно вновь восстановить исходный сигнал. В простейшем случае при дискретизации аналогового сигнала формируется множество его отсчетных значений соответствующей амплитуды (в виде бесконечно коротких импульсов), взятых через интервал времени, отвечающий условию теоремы Котельникова.
, и по которым с заданной точностью можно вновь восстановить исходный сигнал. В простейшем случае при дискретизации аналогового сигнала формируется множество его отсчетных значений соответствующей амплитуды (в виде бесконечно коротких импульсов), взятых через интервал времени, отвечающий условию теоремы Котельникова.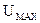 (или от
(или от 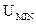 до
до  , называемых шагом квантования. При этом каждому фиксированному уровню сигнала
, называемых шагом квантования. При этом каждому фиксированному уровню сигнала 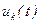 присваивают определенное значение в форме условного числа цифрового кода. С точки зрения удобства технической реализации и обработки обычно используют двоичные цифровые коды, составленные из n (n – целое число) разрядов, каждый из которых представлен «1» – импульсом или «0» – паузой. Общее число уровней квантования составляет 2 n. уровень шага квантования связан с количеством разрядов двоичного кода формулой:
присваивают определенное значение в форме условного числа цифрового кода. С точки зрения удобства технической реализации и обработки обычно используют двоичные цифровые коды, составленные из n (n – целое число) разрядов, каждый из которых представлен «1» – импульсом или «0» – паузой. Общее число уровней квантования составляет 2 n. уровень шага квантования связан с количеством разрядов двоичного кода формулой: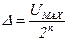 .
. .
.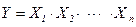 .
. . Словами данная операция трактуется как «игрек не равен иксу» или «игрек равен иксу под чертой»
. Словами данная операция трактуется как «игрек не равен иксу» или «игрек равен иксу под чертой»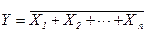 и
и  , при этом на выходе первой схемы при наличии хотя бы одного их слагаемых будет иметь место нулевой уровень выходного напряжения, а при отсутствии сигнала на всех входах – единичный; на выходе второй схемы при наличии всех сомножителей будет иметь место нулевой уровень выходного напряжения, во всех остальных случаях – единичный.
, при этом на выходе первой схемы при наличии хотя бы одного их слагаемых будет иметь место нулевой уровень выходного напряжения, а при отсутствии сигнала на всех входах – единичный; на выходе второй схемы при наличии всех сомножителей будет иметь место нулевой уровень выходного напряжения, во всех остальных случаях – единичный.


