Математические модели элементарных измерительных сигналов
Дельта – функция рассмотрим теоретическую модель бесконечно короткого импульса с бесконечно большой амплитудой, аналитически определяемого формулой:
Площадь такого импульса всегда равна единице, т.к. Функцию При сдвиге дельта-функции по оси времени на интервал
Дельта-функция обладает важнейшим свойством, благодаря которому она получила широкое применение в математике, физике, радио – и измерительной технике. Пусть имеется некоторая непрерывная функция времени
Это выражение характеризует фильтрующее (выделяющее, или стробирующее – от слова «строб» - короткий прямоугольный импульс) свойство дельта-функции, которое используется для представления дискретизированных во времени сигналов с шагом дискретизации Единичная функция. Предельное, упрощенное аналитическое выражение этого сигнала принято записывать так:
Функцию Спектральная плотность гармонического сигнала. Определим спектральную плотность сигнала
Последнее соотношение можно записать в следующем виде:
Итак, гармоническому (в данном случае косинусоидальному) сигналу с конечной амплитудой соответствует дискретный спектр, состоящий их двух линий бесконечно большой амплитуды в виде дельта-функций, расположенных симметрично относительно нуля на частотах
Здесь знак минус – следствие нечетности функции синуса. Экспоненциальный импульс. Это сигнал с «полубесконечной» длительностью и при единичной амплитуде описывается как Постоянный сигнал – самый простой из элементарных сигналов (напряжение, ток).
|


 .
.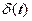 называют дельта-функцией, единичным импульсом, функцией Дирака, и она имеет физическую размерность циклической частоты – с -1.
называют дельта-функцией, единичным импульсом, функцией Дирака, и она имеет физическую размерность циклической частоты – с -1.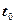 определения функции можно записать в общем виде:
определения функции можно записать в общем виде: ,
,  .
. . Тогда, согласно вышеприведенным формулам, справедливо соотношение:
. Тогда, согласно вышеприведенным формулам, справедливо соотношение: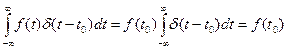
 .
. .
.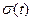 называют единичной функцией, функцией включения или функцией Хевисайда.
называют единичной функцией, функцией включения или функцией Хевисайда. . Подставим в прямое преобразование Фурье заданный сигнал, и, воспользовавшись формулой Эйлера
. Подставим в прямое преобразование Фурье заданный сигнал, и, воспользовавшись формулой Эйлера 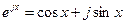 , находим:
, находим: =
= 
 .
. и
и 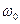 . По аналогии с косинусоидальным сигналом нетрудно показать, что синусоидальному сигналу
. По аналогии с косинусоидальным сигналом нетрудно показать, что синусоидальному сигналу 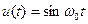 отвечает спектральная плотность
отвечает спектральная плотность .
.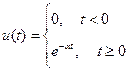 , гле
, гле  - вещественный параметр.
- вещественный параметр.


