Принятие решений в условиях неопределенности. Большинство задач планирования зависит от ряда неизвестных заранее и неуправляемых факторов
Большинство задач планирования зависит от ряда неизвестных заранее и неуправляемых факторов. Эти задачи обладают той или иной степенью неопределенности, которая может быть как объективной, так и субъективной, зависящей от индивидуальных психофизических параметров ЛИР. В таких задачах неизвестно распределение вероятностей p(Zj), с которыми внешняя среда может находиться в одном из возможных состояний Таким образом, для ЛПР, действующего в условиях неопределенности и невозможности получения дополнительной информации о неопределенных факторах, элементами описания ситуации планирования являются: · множество допустимых стратегий (множество возможных альтернатив действий ЛПР) А={A1,A2,…,Am}; · множество возможных состояний внешней среды (множество гипотез) Z={Z1,Z2,…,Zm}. Предполагается, что на множестве отношений А х Z можно задать некоторую функцию полезности f (Ai,Zj), которая выступает в качестве меры желательности или полезности соответствующей альтернативы. Если множества A и Z конечны, то мера для оценки эффективности действий ЛПР (полезность исходов) представима в виде матрицы. Каждое конкретное значение элемента матрицы eij= f (Ai,Zj) (см. табл. 1) характеризует выбор i-й стратегии (альтернативы Ai) при состоянии внешней среды Zj. Для выбора лучшей стратегии имеется ряд специальных методов, ориентированных на использование в условиях неопределенности, которые рассмотрены и проиллюстрированы ниже. Критерий максимина (принцип гарантированного результата, или критерий Вальда). Данный принцип заключается в выборе в качестве оптимальной (наиболее эффективной) той альтернативы (стратегии), которая имеет наибольшее среди наименее благоприятных состояний внешней среды значение функции полезности. Таким образом, оптимальной, считается альтернатива A*, для которой выполняется соотношение:
Здесь eij есть значение функции полезности при альтернативе Рассмотрим следующий пример. Исходная таблица решений характеризуется данными, привёденными в табл. 5. Таблица 5
|

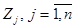 . В этом случае ЛДР выдвигает только определенные гипотезы относительно состояний внешней среды.
. В этом случае ЛДР выдвигает только определенные гипотезы относительно состояний внешней среды.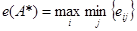 (7)
(7)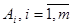 и состоянии внешней среды
и состоянии внешней среды 


