Ожидаемые значения прибыли (тыс.ден.ед.) для трех товарных рынков
Сначала для каждой альтернативы выбираем по соответствующей строке минимальное значение функции полезности, т.е. min{e1j}= min{530,460,240,220 }= 220; min{e2j}= min{490,390,300,270}=270; min{e3j}= min{575,420,2б0,190}=190. Далее из полученных минимальных значений в соответствии с (7) выбирается максимальное: max{220,270,190} = 270 (для i=2).
Следовательно, оптимальной по критерию максимина является альтернатива А2, т.е. фирме целесообразно выходить со своим товаром на рынок А2. Это самая осторожная стратегия, так как при любом состоянии внешней среды фирма получит прибыль не менее 270 тыс.ден.ед.
Критерий максимакса (принцип безудержного оптимизма). Если критерий максимина ориентирован на получение гарантированного минимума желаемого результата (правило "лучший" из "худших”), то критерий оптимизма предполагает возможность получения максимального уровня желательности результата. Эта альтернатива А* выбирается исходя из выражения
Рассматривая исходные данные (табл. 5) с точки зрения принципа оптимизма (8), получим: max{e1j}= max{530,460,240,220 }= 530; max{e2j}= max{490,390,300,270}=490; max{e3j}= max{575,420,2б0,190}=575; max{530,490,575} = 575 (для i=3). Таким образом, оптимальной по критерию оптимизма будет альтернатива А3, для которой справедливо соотношение: e(A*)=e(A3)=max max eij = 575.
Критерий Гурвица. Данный критерий представляет собой комбинацию принципа гарантированного результата и принципа оптимизма. Функция, описывающая критерий Гурвица, представляется в виде:
где е1(А) - стратегия выбора альтернативы, характеризующая принцип гарантированного результата, а e2(A) - принципа оптимизма; Так как то общее выражение для принципа Гурвица на основании (9) будет иметь следующий вид:
Здесь используются две гипотезы: первая - среда находится с вероятностью а в самом невыгодном состоянии и вторая- среда находится с вероятностью В зависимости от значения весового коэффициента Используя этот критерий, обратимся опять к нашим данным (табл. 5). Пусть весовой коэффициент, характеризующий степень важности соответствующей альтернативы, равен 0,7. Тогда получим:
Подставляя значения из табл. 6.5 в выражение (6.10), имеем: e(A1)= 0,7 х 220 + 0,3 х 530 =154+159 = 313; e(A2)= 0,7 х 270 + 0,3 х 490 =189 + 147=336; e(A3)= 0,7 х 190 + 0,3 х 575 =133+172,5 = 305,5. Далее производим выбор на основе следующей стратегии:
Подставляя вычисленные ранее значения, получим: е (A*) = mах [313; 336; 305,5] = 336 (для i= 2). Таким образом, оптимальной по принципу Гурвица при коэффициенте Приведем решение данным методом в следующей таблице:
Если же весовой коэффициент равен 0,2 то решение изменится следующим образом: e(A1)= 0.2 х 220 + 0,8 х 530 =44+424=468; e(A2)= 0,2 х 270 + 0,8 х 490 =54+393=446; e(A3)= 0,2 х 190 + 0,8 х 575 =38+460=498; е (A*) = mах [468,446,498] = 498 (i= 3). Оптимальной стратегией в этом случае будет работа фирмы на рынке A3. Приведем решение в виде таблицы:
Наконец, если положить e(A1)=375; e(A2)=380; e(A3)=382,5, е (A*) = mах [375,380,382,5] = 382,5 (i= 3). И в этом случае оптимальной стратегией будет работа на рынке A3. Приведем решение в виде таблицы:
Заметим, что если фирма желает, например, работать на всех трех рынках, то, используя принцип Гурвица, можно принять следующее решение по распределению долей продукции (долей объемов продаж) между рынками, применив формулу:
где di. - доля товара в натуральном или денежном выражении, реализуемого на рынке Ai, i=1,2,3. В общем случае процентное соотношение распределения товара по рынкам с использованием критерия Гурвица может быть вычислено по аналогичной формуле:
где Di - доля товара, реализуемого на рынке Ai, выраженная в процентах; m - количество рассматриваемых рынков. В нашем примере при
Однако представляется более рациональным распределить товар между рынками A2 и А3, так как рынок A2 должен быть выбран согласно принципу гарантированного результата, а рынок A3 - согласно принципу оптимизма, причем изменение весового коэффициента в принципе Гурвица приводит к тем же альтернативам A2 и A3. Поэтому, используя формулу (11) для двух рынков и
Вообще говоря, здесь мы имеем пропорциональное распределение рисков. Данный подход может быть использован в практических расчетах.
Критерий минимаксного сожаления (принцип Сэвиджа). Стратегия выбора по принципу Сэвиджа характеризует те потенциальные потери, которые фирма будет иметь, если выберет неоптимальное решение. Детализированная процедура выбора в этом случае производится в три этапа.
1. Для каждого состояния внешней среды по конкретной альтернативе определяется максимальное значение функции полезности:
Это есть, возможно, наилучший уровень полезности, который можно получить для конкретного состояния внешней среды Zj. 2. На основании значений, вычисленных по формуле (6.12), для каждой альтернативы строится показатель:
Данный показатель характеризует потенциальный риск, а точнее потерянную выгоду от выбора неоптимальной альтернативы. В результате этого действия формируется матрица потенциальных потерь. 3. Используя полученную на предыдущем этапе матрицу потерь (или, как еще говорят, матрицу сожалений), производится выбор стратегии с наименьшим показателем риска:
Данный критерий минимизирует возможные потери при условии, что состояние внешней среды наихудшим образом отличается от предполагаемого. Рассмотрим применение принципа Сэвиджа на исходных данных (табл. 6.5) в соответствии с описанной выше процедурой. 1. Для значений функции полезности по каждому состоянию внешней среды Z1, Z2, Z3, Z4 на основании (12) определим максимальный уровень полезности: mах{ei1} = mах {530; 490; 575} = 575; mах {ei2} = mах {460; 390; 420} = 460; max{ei3} = mах {240; 300; 260} = 300; mах {ei4} = mах {220; 270; 190} = 270.
2. Вычислим элементы матрицы потенциальных потерь согласно формуле (6.13): w (е11)= 575 - 530 = 45; w (е13)= 300 - 240 = 60; w (е21)= 575 - 490 = 85; w (е23)= 300 - 300 = 0; w (е31)= 575 - 575 = 0; w (е33)= 300 - 260 = 40; w (е12)= 460 - 460 = 0; w (е14)= 270 - 220 = 50; w (е22)= 460 - 390 = 70; w (е24)= 270 - 270 = 0; w (е32)= 460 - 420 = 40; w (е34)= 270 - 190 = 80. Таким образом, матрица потерь будет иметь следующий вид (табл. 6). Таблица 6
|

 (8)
(8) (9)
(9)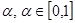 - весовой коэффициент.
- весовой коэффициент.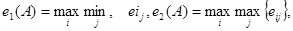
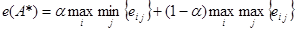 или
или
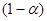 в самом выгодном состоянии.
в самом выгодном состоянии. можно получить различные предпочтительные альтернативы. Причем если
можно получить различные предпочтительные альтернативы. Причем если  , то имеем принцип оптимизма, если
, то имеем принцип оптимизма, если  , то получим принцип гарантированного результата.
, то получим принцип гарантированного результата. (10)
(10)
 будет альтернатива A2.
будет альтернатива A2.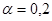
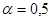 , то получим следующее решение:
, то получим следующее решение: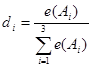
 (11)
(11)

 (12)
(12) (13)
(13)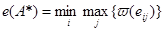 (14)
(14)


