Матрица потенциальных потерь
3. На основании матрицы потерь (табл. 6) можно определить максимальные потери по каждой альтернативе. Для этого применим правило:
Для каждого i= 1,2,3 определим: w (A1)= mах [45; 0; 60; 50] = 60; w (A2)= mах [85; 70; 0; 0] = 85; w (A3)= mах [0; 40; 40; 80] = 80.
Оптимальной будет та альтернатива, которая имеет минимальные потери согласно выражению (6.14):
w (A*) = min{60; 85; 80}= 60. Следовательно, оптимальна альтернатива A1 имеющая минимальные потери выгоды. Критерий Лапласа. Данный критерий применяется, если состояния внешней среды неизвестны, но их можно считать равновероятными, т. е.
Решающее правило в этом случае имеет следующий вид:
В рассматриваемом примере: е (A*) = mах{(530+460+240+220) / 4; (490+390+300+270) / 4; (575+420+260+190) / 4} = =mах {362,5; 362,5; 361,25} = 362,5. Следовательно, с точки зрения критерия Лапласа можно выбрать как рынок A1, так и рынок A2.
Сделаем несколько практических рекомендаций по применению рассмотренных выше критериев (принципов). 1. Критерий Вальда лучше всего использовать тогда, когда фирма желает свести риск от принятого решения к минимуму. 2. Коэффициент в критерии Гурвица выбирается из субъективных соображений: чем опаснее ситуация, тем больше ЛПР желает подстраховаться. 3. Критерий Сэвиджа удобен, если для предприятия приемлем некоторый риск. 4. Критерий Лапласа может быть применен, когда ЛПР не может предпочесть ни одной гипотезы. Методы планирования в условиях риска Когда выбор планового решения осуществляется в условиях риска, известны или задаются субъективные вероятности возможных состояний внешней среды. При этом постановка задачи будет следующей: а) имеется множество альтернатив A={A1, A2, …, Am} и множество состояний внешней среды Z={Z1, Z2, …, Zn}; б) известны субъективные вероятности состояния среды (р(Z1), р(Z2),..., р(Zn)) =(p1, p2, …, pn), причем в) для каждого сочетания альтернативного решения Ai и состояния Zj задана функциональная полезность eij. Исходная информация представляется в виде табл. 6.1. Существующие методы выбора базируются в основном на использовании вероятностных мер в качестве критериев выбора. В теории статистических решений обычно используются принцип Байеса. принцип Бернулли и принцип энтропии математического ожидания функции полезности. Принцип Байеса. В качестве критерия выбора стратегии (альтернативы) Ai применяются взвешенные по вероятности суммы полезностей, т. е.
Оптимальным считается решение A*, для которого значение критерия ei будет максимальным или минимальным в зависимости от постановки задачи:
или
Если в примере (табл.6.5) задать вероятности p1=0,4; p2=0,2; р3=0,1; р4=0,3, то на основе (6.15) и (6.16) получим: e1 = 530 х 0,4+460 х 0,2 + 240 х 0,1 + 220 х 0,3 = 394; e2 = 490 х 0,4+390 х 0,2 + 300 х 0,1 + 270 х 0,3 = 385; e3 = 575 х 0,4+420 х 0,2 + 260 х 0,1 + 190 х 0,3 = 397; max{394,385,397}=397 (для i=3). Следовательно, оптимальной является альтернатива A3.
Иногда каждому решению A1, ставят в соответствие не значение функции полезности eij, а величину потерь w ij = |eij-max{eij}|, которая характеризует упущенные возможности. Тогда
Используя матрицу потенциальных потерь (табл. 6.6), вычислим с учетом вероятностей наступления тех или иных состояний среды общие потери: w 1= 0,4 х 45 + 0 + 0,1 х 60 + 0,3 х 50 = 39; w 2= 0,4 х 85 + 0,2 х 70 + 0 + 0 = 48; w 3= 0+0,2 х 40 + 0,1 х 40 + 0,3 х 80 = 36. На основе формулы (6.17) имеем: min { w 1, w 2, w 3) = min {39; 48; 36}= 36 (для i=3). Оптимальной альтернативой является A3.
Принцип Бернулли. При использовании данного принципа исходят из того, что известна некоторая функция полезности u(е). Эта субъективная функция полезности Бернулли ставит в соответствие каждому возможному вероятностному значению альтернативы определенную величину полезности. Для каждой альтернативы можно определить ожидаемое значение полезности ее вероятностного результата. Оптимальной считается альтернатива с наибольшим ожидаемым значением полезности, т. е. оптимальной стратегии
Вид функции полезности Бернулли зависит от отношения ЛПР к риску. Принципиальный вид функции полезности: а) при нейтральном (безразличном) отношении к риску; б) при существенном учете риска; в) при малой значимости риска представлен на рис.2. Здесь следует заметить, что на различных интервалах изменения аргумента функция полезности может иметь различный вид с точки зрения отношения к риску. Рассмотрим принцип Бернулли применительно к задаче, исходные данные которой представлены в табл.6.5, а вероятности состояния внешней среды такие же, как и в примере, иллюстрирующем принцип Байеса, а именно р1= 0.4; p2= 0,2; p3=0,1; р4=0,3. В результате проведенных расчетов функция полезности Бернулли имеет следующий вид:
Рис. 2. Вид функции полезности Бернулли при различных точках зрения на риск График данной функции изображен на рис.3. Результаты определения оптимальной альтернативы (нового целевого рынка) по принципу Бернулли помещены в табл. 7. Таблица 7
|

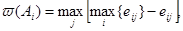


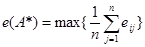
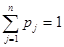 .
. (15)
(15)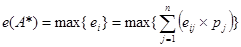 (16)
(16)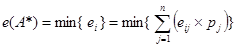
 (17)
(17)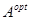 соответствует
соответствует





