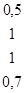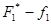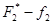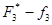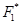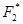Матрица исходных данных для многокритериальных методов выбора
Однако, как было отмечено ранее, доминирующие стратегии т практике встречаются довольно редко. Поэтому приходится применять методы многокритериального выбора, причем решение должно быть наилучшим в определенном смысле. Итак, выделение существенных для модели рассматриваемой экономической системы показателей качества альтернатив выбора, соответствующих поставленным целям, приводит к задаче векторной оптимизации, которая заключается в нахождении максимума вектор-функции:
где D – область допустимых решений модели. В случае многокритериальной оптимизации возникают три проблемы. Первая проблема связана с выбором принципа оптимальности. В математическом отношении эта проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности - выбору отношений порядка. Вторая проблема связана с нормализацией векторного критерия F(х). Дело в том, что частные критерии имеют различные единицы измерения, поэтому их необходимо привести к единому масштабу измерения, т. е. нормализовать(обычно приводят к безразличным величинам). Третья проблема связана с учетом приоритета (степени важности) частных критериев. Часто для учета приоритета вводится вектор распределения важности или значимости критериев В задаче многокритериального выбора решение почти всегда ищется в области компромиссов или в области решений, оптимальных по Парето, Известен целый ряд методов решения многокритериальных задач, которые можно разбить на четыре группы: 1. Сведение многих критериев к одному путем введения весовых коэффициентов для каждого критерия (более важный критерий получает больший вес). 2. Минимизация максимальных отклонений от наилучших значений по всем критериям. 3. Оптимизация одного критерия (почему-либо признанного наиболее важным), а остальные критерии выступают в роли дополнительных ограничений. 4. Упорядочение (ранжирование) множества критериев и последовательная оптимизация по каждому из них. В рассматриваемой постановке множество допустимых планов есть совокупность альтернатив f j(Ai)= e ij. Покажем применение некоторых методов многокритериальной оптимизации к решению задач планирования в системе управления фирмой. Метод равномерной оптимизации:
Он применяется, если глобальное качество альтернативы представляет собой сумму локальных (частных) качеств и, кроме того, все критерии имеют одну и ту же единицу измерения, например денежное выражение либо безразмерные величины. Главный недостаток метода -это возможность компенсации малых значений некоторых критериев достаточно большими значениями других. Метод справедливого компромисса:
Он применяется, во-первых, потому что существуют разнообразные схемы, приводящие к такому методу, во-вторых, потому что имеется тесная связь с решением в некооперативных играх. Метод свертывания критериев:
Здесь каждому из критериев приписываются весовые коэффициенты а, определяющие предпочтения ЛПР. Метод главного критерия:
Здесь f 1(х) - главный (наиболее важный из всех для ЛПР) критерий, d j- нижняя граница j-го критерия, устанавливаемая ЛПР. Метод идеальной точки. Ищется план, удовлетворяющий условию равномерного сжатия:
Метод последовательных уступок (или пороговых значений):
где h j - уступка по критерию f j(x), т. е. величина, на которую ЛПР согласен уменьшить значение данного критерия по сравнению с его максимальным значением. Метод группировки критериев. Суть метода заключается в том, что множество критериев, значения которых предварительно вычислены на некотором оптимальном по Парето плане x °, разбивается на три группы. Первая группа включает критерии, значения которых могут быть уменьшены по сравнению со значениями, вычисленными на плане x ° Вторая группа состоит из критериев, значения которых желательно увеличить. Третья группа включает критерии, значения которых не хотелось бы уменьшать по сравнению с достигнутыми на плане x °. Далее отыскивается план уже в новой системе ограничений, который позволяет максимально увеличить значение критерия второй группы. Так как критерии могут иметь различные масштабы и шкалы измерения, то прежде, чем приступить к решению многокритериальной задачи, их необходимо привести к одной единице измерения (обычно к безразмерному виду). Этот процесс называется нормализацией. Существуют различные методы нормализации, Предлагается следующий способ получения безразмерной формы критериев:
где
Рассмотрим следующую многокритериальную задачу планирования. Пусть фирма имеет возможность реализовывать свои товары на 4-х различных рынках (альтернативы А1, А2, А3, А4). При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимальный объем продаж в течение планируемого периода. Исходные данные приведены в табл. 3. Таблица 3 Исходные данные многокритериальной задачи (пример)
Значения критериев даны в различных единицах измерения, поэтому согласно формуле (6) приведем их к безразмерному виду:
Так как критерий f 1, минимизируется, то для того, чтобы все критерии стремились к максимуму, умножим безразмерные величины критерия f 1, на (-1) и сформируем табл. 4. Решим задачу несколькими методами. Таблица 4 Преобразованные исходные данные (пример)
Метод равномерной оптимальности. В соответствии с (1) имеем:
Следовательно, согласно принципу равномерной оптимальности предприятию выгоднее работать на рынке А1 Метод справедливого компромисса. Чтобы воспользоваться данным методом, избавимся от отрицательности критерия f 1, добавив константу, например 1. Тогда значения первого критерия будут равны:
На основании (2) имеем: mах{0,5 х 0,5 х1; 1 х 0 х 0.5; 0; 0,75 x 0,5 х 0,3}=mах{0,25; 0; 0; 0,1125}= 0,25.
Результат получился аналогичный предыдущему, а именно выгоднее работать на рынке А1. Метод свертывания критериев. Сначала положим следующие значения весовых коэффициентов: f 1= -0,5х0,2+0,5х0,3+1 х 0,5= 0,55; f 2= 0х0,2+0х0,3+0,5х0,5=0,25; f 3= -1х0,2+1х0,3+0х0,5=-0,2 + 0,3+0=0,1; f 4= -0,25х0,2+ 0,5х0,3 + 0,3х0,5= 0,25; mах{ 0,55; 0,25; 0,1; 0,25} = 0,55.
При таком значении коэффициентов значимости критериев выгоднее работать на рынке A1 Если доложить f 1= -0,5х0,1+0,5х0,7+1х0,2= 0,5; f 2= 0х0,1+0х0,7+0,5х0,2=0,1; f 3= -1х0,1+1х0,7+0х0,2=0,6; f 4= -0,25х0,1+ 0,5х0,7 + 0,3х0,2= 0,385; mах{ 0,5; 0,1; 0,6; 0,385} = 0,6.
Таким образом, если приоритет отдается доле рынка ( Если же фирма находится в затруднительном положении с точки зрения средств, выделяемых на рекламу, другими словами, для нее в данный момент самым важным является минимизация затрат на рекламу, то коэффициенты значимости могут быть, например, выбраны такие: Следовательно, в такой ситуации лучше всего работать на рынке А2. Если задать весовые коэффициенты f 1=-0,35; f 2=0,15; f 3=0,1; f 4=0,215; mах {0,35; 0,15; 0,1; 0,215) =0,35. При таких значениях весовых коэффициентов выгоднее работать на рынке А1 Приведем два последних варианта решений в следующей таблице:
Метод главного критерия. Пусть главный критерий f 1 - затраты на рекламу, а остальные критерии выступают в роли ограничений, причем доля рынка должна быть не меньше 45%, а объем продаж не меньше 85 тыс.ден.ед. Тогда в соответствии с (6.4) минимальное значение главного критерия f 1 равно 5 тыс.ден.ед. и соответствует альтернативе А2 однако с учетом ограничения на долю рынка следует выбрать альтернативу A4, но так как еще требуется, чтобы объем продаж был не меньше 85 тыс.ден.ед., то наилучшей альтернативой в этом случае будет рынок A1. f1-главный критерий,
Метод идеальной точки (критерий равномерного сжатия (6.5) соответствует принципу Сэвиджа). Определим сначала максимальные значения критериев. А именно max
Максимальные отклонения по каждой из 4-х альтернатив имеют следующие значения: 0,5; 1; 1; 0,7. Выберем минимальное из этих отклонений: min {0,5; 1;1; 0,7}=0,5.
Минимальное значение 0,5 соответствует альтернативе A1 следовательно, используя данный метод, получим решение, которое рекомендует фирме планировать работу на рынке A1.
|

 ,
, .
. , а значения критериев равны:
, а значения критериев равны: (1)
(1)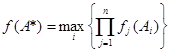 (2)
(2)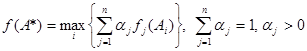 (3)
(3)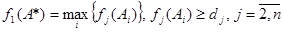 (4)
(4)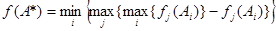 (5)
(5)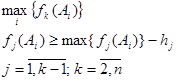
 (6)
(6)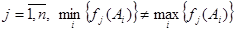
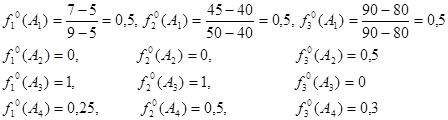

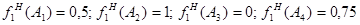
 .Тогда функции свертки в соответствии с (6.3) будут равны:
.Тогда функции свертки в соответствии с (6.3) будут равны: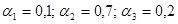 , то получим:
, то получим: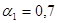 ), то фирме имеет смысл работать на рынке А3.
), то фирме имеет смысл работать на рынке А3.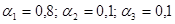 ; mах {-0,25;0,05;-0,7;-0,12}=0,05.
; mах {-0,25;0,05;-0,7;-0,12}=0,05.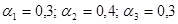 , то
, то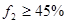 ,
, 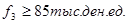
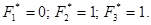 Матрица отклонений значений критериев от наилучших значений имеет вид:
Матрица отклонений значений критериев от наилучших значений имеет вид: