Начало.
Шаг 1. Ввод исходных данных игровой модели: множества вариантов {Bj},  , предполагаемых действий игрока N ("противника") и соответствующих значений j степеней уверенности о выборе игроком N той или иной стратегии, множества матриц выигрышей участников коалиции и т.д.
, предполагаемых действий игрока N ("противника") и соответствующих значений j степеней уверенности о выборе игроком N той или иной стратегии, множества матриц выигрышей участников коалиции и т.д.
Шаг 2. Определение игроком 1 (старшим игроком коалиции) стратегии, обеспечивающей его наибольший выигрыш следующим образом.
При помощиалгоритма нечеткого логического вывода типа Мамдани [6] определяется значение выигрыша при выборе игроком A1 любой чистой стратегии A1i  :
:
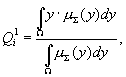 (6)
(6)
где
 (7)
(7)
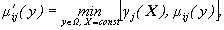 (8)
(8)
– область определения y, X в выражении (8) полагается константой, отражающей результаты эксперимента (разведки), а степени принадлежности j, ij и т.д. относятся к матрице выигрышей первого игрока.
Очевидно, первый игрок A1 должен выбирать стратегию A1g*, обеспечивающую наибольший выигрыш:
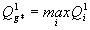 (9)
(9)
С учетом изложенного, алгоритм решения поставленной задачи при известных  и измеренном значении X сводится к расчету по формулам (6) – (9) величин выигрыша для различных возможных стратегий игрока A1 и выбору, в соответствии с этими расчетами, стратегии, для которой этот выигрыш является наибольшим.
и измеренном значении X сводится к расчету по формулам (6) – (9) величин выигрыша для различных возможных стратегий игрока A1 и выбору, в соответствии с этими расчетами, стратегии, для которой этот выигрыш является наибольшим.
Шаг 3. Определение игроком 2 (следующим по старшинству в коалиции после игрока 1) стратегии, обеспечивающей его наибольший выигрыш с учетом выбора игрока 1, т.е. с использованием соответствующей частной матрицы выигрышей и методики отмеченной выше.
…
Шаг N. Определение игроком N-1 (младшим членом коалиции) стратегии, обеспечивающей его наибольший выигрыш с учетом выбора предыдущих участников коалиции.
Шаг N+1. Вывод итоговых результатов – конечного набора стратегий участников коалиции и значений ожидаемых выигрышей.
Конец.
Следует отметить, что данный алгоритм применим только для строго иерархической коалиции, в которой наибольший выигрыш, вообще говоря, получают старшие члены коалиции.

 , предполагаемых действий игрока N ("противника") и соответствующих значений j степеней уверенности о выборе игроком N той или иной стратегии, множества матриц выигрышей участников коалиции и т.д.
, предполагаемых действий игрока N ("противника") и соответствующих значений j степеней уверенности о выборе игроком N той или иной стратегии, множества матриц выигрышей участников коалиции и т.д. :
: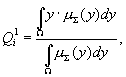 (6)
(6) (7)
(7)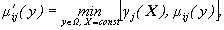 (8)
(8)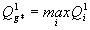 (9)
(9) и измеренном значении X сводится к расчету по формулам (6) – (9) величин выигрыша для различных возможных стратегий игрока A1 и выбору, в соответствии с этими расчетами, стратегии, для которой этот выигрыш является наибольшим.
и измеренном значении X сводится к расчету по формулам (6) – (9) величин выигрыша для различных возможных стратегий игрока A1 и выбору, в соответствии с этими расчетами, стратегии, для которой этот выигрыш является наибольшим.


