Эффективность коалиционной структуры определяет их общий выигрыш, который зависит от распределения игроками средств в количестве единицы между нечеткими коалициями.
Для оптимизации эффективности коалиционной структуры решаем задачу линейного программирования, в которой искомыми переменными являются величины перераспределения средств каждым игроком между коалициями структуры, и коэффициенты разложения каждой из этих нечетких коалиций в выпуклую комбинацию четких коалиций.
Итоговым результатом данной теории является методика, позволяющая учесть частичное присутствие игрока в коалиции.
Возможность формирования структуры, состоящей из нечетких коалиций, позволяет моделировать объединение игроков для участия в нескольких проектах одновременно любой долей своих средств.
Данная методика позволяет найти оптимальное распределение средств игрока между проектами, гарантирующее получение совместного наибольшего выигрыша.
Проведенный обзор работ и изучение практических задач позволяет конкретизировать задачу построения коалиционной игровой модели для выбора инновационной стратегии интеграционного образования развития исследования следующим образом:
1) в общем случае в игре принимают участие N игроков, при этом коалицию образуют N -1 участник против одного игрока ("противника"),
2) игра носит уникальный характер,
3) игра содержит элементы неопределенности (т.е. неполную информированность о возможных действиях противника, о величине выигрыша или потерь при выборе той или иной стратегии и т.п.), которые трудно или невозможно отразить категориями теории вероятностей, но можно выразить в лингвистической форме;
Примем следующую математическую формулировку нечеткой игровой модели.
Дано:
1) множество вариантов { Bj },  , предполагаемых действий игрока N ("противника");
, предполагаемых действий игрока N ("противника");
2) множество вариантов или стратегий { Asi }, 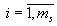 ,
, 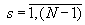 , s -го участника коалиции;
, s -го участника коалиции;
* Замечание: { Bj } и { Asi } – это инновационные стратегии, означающие выполнение определенной последовательности действий;
3) набор признаков { xk },  среди которых могут быть как количественные (непрерывные), так и качественные (дискретные);
среди которых могут быть как количественные (непрерывные), так и качественные (дискретные);
4) набор функций принадлежности jk(xk), отражающих степени уверенности, что при фактически наблюдаемом признаке x*k игроком N будет избран вариант поведения Bj, или набор значений j степеней уверенности о выборе игроком N той или иной стратегии;
5) набор термов (т. е. имен) asij, 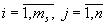 , лингвистической переменной "выигрыш" (выигрыш игрока s), например, as11 – "малый выигрыш", as12 – "большой выигрыш" и т.п., задаваемый с учетом стратегий выбранных предыдущими (s –1)- м участниками коалиции;
, лингвистической переменной "выигрыш" (выигрыш игрока s), например, as11 – "малый выигрыш", as12 – "большой выигрыш" и т.п., задаваемый с учетом стратегий выбранных предыдущими (s –1)- м участниками коалиции;
6) набор степеней принадлежности мsij, соответствующих термам asij.
Требуется: найти стратегии Asg* участников коалиции, обеспечивающие их наибольший выигрыш в результате реализации инновационной стратегии развития с учетом возможных действий противника и других участников коалиции.
Возможные алгоритмы решения.
Выбор того или иного алгоритма решения сформулированной задачи определяется в основном условиями распределения выигрыша между участниками коалиции. Здесь возможны следующие ситуации.
1. Участники коалиции проранжированы по их важности и делают ходы (выбирают свои стратегии) по очереди, имея информацию о стратегии, выбранной предыдущими (более "важными") членами коалиции, т.е. сначала стратегию выбирает первый участник, затем, зная его выбор – второй, далее, с учетом стратегий двух первых – третий и т.д. В этом случае критерий эффективности общей коалиционной стратегии распадается на частные критерии вида:
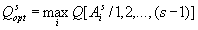 , (3)
, (3)
где  – выигрыш s-го игрока при условии, что им выбрана наилучшая стратегия из возможных (
– выигрыш s-го игрока при условии, что им выбрана наилучшая стратегия из возможных ( ) при сделанном выборе предыдущими (s-1)-м членами коалиции. Заметим, что число платежных матриц, например, 2-го по значимости участника коалиции необязательно равно числу возможных стратегий первого (самого старшего) участника и т.д.
) при сделанном выборе предыдущими (s-1)-м членами коалиции. Заметим, что число платежных матриц, например, 2-го по значимости участника коалиции необязательно равно числу возможных стратегий первого (самого старшего) участника и т.д.
2. Участники коалиции обмениваются информацией о своих предполагаемых действиях и согласуют их до выработки окончательного решения. В этом варианте, который можно назвать демократическим, в качестве критерия принимается суммарный выигрыш всех участников коалиции, возможно, с учетом некоторых весовых коэффициентов, определяемых заранее и отражающих значимость каждого из членов коалиции:
Qopt = 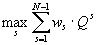 , (4)
, (4)
где Qs – выигрыш s-го члена коалиции, ws – отмеченные весовые коэффициенты, такие, что
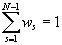 . (5)
. (5)
В соответствии с изложенным, можно предложить два алгоритма решения коалиционной игры, соответствующих рассмотренным выше двум видам принятия решений по выбору инновационной стратегии развития в рамках интеграционного образования..

 , предполагаемых действий игрока N ("противника");
, предполагаемых действий игрока N ("противника");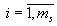 ,
, 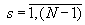 , s -го участника коалиции;
, s -го участника коалиции; среди которых могут быть как количественные (непрерывные), так и качественные (дискретные);
среди которых могут быть как количественные (непрерывные), так и качественные (дискретные);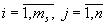 , лингвистической переменной "выигрыш" (выигрыш игрока s), например, as11 – "малый выигрыш", as12 – "большой выигрыш" и т.п., задаваемый с учетом стратегий выбранных предыдущими (s –1)- м участниками коалиции;
, лингвистической переменной "выигрыш" (выигрыш игрока s), например, as11 – "малый выигрыш", as12 – "большой выигрыш" и т.п., задаваемый с учетом стратегий выбранных предыдущими (s –1)- м участниками коалиции;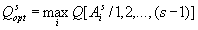 , (3)
, (3) – выигрыш s-го игрока при условии, что им выбрана наилучшая стратегия из возможных (
– выигрыш s-го игрока при условии, что им выбрана наилучшая стратегия из возможных ( ) при сделанном выборе предыдущими (s-1)-м членами коалиции. Заметим, что число платежных матриц, например, 2-го по значимости участника коалиции необязательно равно числу возможных стратегий первого (самого старшего) участника и т.д.
) при сделанном выборе предыдущими (s-1)-м членами коалиции. Заметим, что число платежных матриц, например, 2-го по значимости участника коалиции необязательно равно числу возможных стратегий первого (самого старшего) участника и т.д.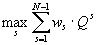 , (4)
, (4)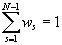 . (5)
. (5)


