Маршрут, длина маршрута. Цепи. Простые цепи. Контур. Цикл.
Лекция № 6. Маршрут, длина маршрута. Цепи. Простые цепи. Контур. Цикл. Простые и элементарные циклы. Ациклический граф. Понятие связности. Компоненты связности. Эйлеровы графы. Теорема Эйлера о существовании Эйлерова цикла. Гамильтоновы графы. Достаточные условия существования гамильтонова цикла в графе. Маршрут, длина маршрута. Цепи. Простые цепи. Контур. Цикл. Маршрут в графе – это последовательность вершин и рёбер Рёбра и вершины в маршруте могут повторяться. Если начальная и конечная вершины совпадают, то маршрут называется замкнутым. Если все вершины и рёбра маршрута различны, то он называется цепью. Замкнутая цепь - это цикл. Длина маршрута равна числу входящих в него рёбер. Вершина vj называется достижимой из вершины vi, если vi = vj, или существует путь из вершины vi в вершину vj. Определение. Вершина w орграфа D (графа G) достижима из вершины v, если либо v=w, либо существует путь из v в w(маршрут, соединяющий v, w). Вершина vj называется достижимой из вершины vi, если vi = vj, или существует путь из вершины vi в вершину vj.
Введем понятие маршрута для графа G = (V, E) (и соответственно понятие пути для орграфа D = (V, E)). Определение. Маршрутом в данном графе G называется конечная последовательность ребер вида {v0, v1}, {v1,v2}, …, {vm-1, vm} (обозначаемая также v0®v1®v2®…®vm). Каждому маршруту соответствует последовательность вершин v0v1v2…vm; v0 – начальная вершина, а vm – конечная вершина маршрута. Одна и та же вершина может одновременно оказаться начальной, конечной и внутренней. Таким образом, мы будем говорить о маршруте из v0 в vm. Определение. Длиной маршрута называется число ребер в нем. Определение. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все вершины тоже различны (кроме, может быть, начальной и конечной вершин). Определение. Цепь или простая цепь замкнуты, если начальная и конечная вершины совпадают. Определение. Замкнутая простая цепь, содержащая, по крайней мере, одно ребро, называется циклом. Определение. Обхватом графа называется длина его кратчайшего цикла. Пусть Путь в графе - это символ вида
где Определение. Путем в графе (орграфе) называется последовательность в которой чередуются вершины и дуги графа. Начинается последовательность с вершины которая называется началом пути и заканчивается вершиной, называемой концом пути. Например, для графа изображенного на рис.3.11, путем будет следующая последовательность: v1 x1 v2 x3 v4 x4 v3, где v1- начало, а v3- конец пути.
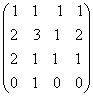
Рис. 3.11 Замечание. Путь можно записать по последовательности дуг, которые входят в данный путь. Для приведенного выше пути, это будет последовательность: x1 x3 x4. Если дуги имеют кратность 1, то путь можно записать по последовательности вершин, входящих в данный путь. Для приведенного выше пути, это будет последовательность: v1 v2 v4 v3. Определение. Длиной пути называется число дуг, входящих в данный путь. Длина приведенного выше пути – 3. Путь называется замкнутым, если начало пути совпадает с концом этого пути. Определение. Цепью называется путь в котором все дуги различны. Простая цепь – цепь в которой все вершины различны. Определение. Циклом (контуром) в графе (в орграфе) называется замкнутая цепь. Простой цикл (контур) – цикл (контур) в котором все вершины различны. З а мечание. Начало и конец пути в замкнутом контуре считается за одну вершину. Для графа рис.3.11 путь v2 x3 v4 x4 v3 x2 v2 x1 v1 является цепью длиной 4, путь v1 x1 v2 x3 v4 x Справедливы следующие утверждения: Утверждение 1. В псевдографе (в ориентированном псевдографе) из всякого замкнутого пути можно выделить простой цикл. Утверждение 2. Из всякого незамкнутого пути можно выделить простую цепь с тем же началом и концом. Например, для графа рис.3.11 из замкнутого пути v1 x1 v2 x3 v4 x4 v3 x2 v2 x1 v1 можно выделить простой цикл v2 x3 v4 x4 v3 x2 v2, а из пути v2 x3 v4 x4 v3 x2 v2 x1 v1 можно выделить простую цепь v2 x1 v1 с тем же началом и концом. Утверждение 3. Элемент a На рис.3.12 показан граф и его матрица смежности.
Рис. 3.12 Матрицы А A Элемент a Утверждение 4. Для того чтобы n – вершинный граф (орграф) имел хотя бы один цикл (контур), необходимо и достаточно, чтобы матрица K = A Замечани е. Утверждение 4 справедливо и для ориентированного n – вершинного псевдографа, причем в этом случае K = A + A На рис.3.13 показан ориентированный псевдограф и его матрица смежности.
Рис. 3.13 Матрицы A A Элемент a v1 x2 v2 x4 v3 x6 v4 и v1 x2 v2 x3 v2 x7 v4. Из вершины v2 в вершину v1 имеется 5 путей длиной 3, т.к. в матрице A Для данного псевдографа матрица K = A + A Следствие 1. В графе (орграфе) тогда и только тогда существует путь из вершины vi в вершину vj, когда (i, j) - й элемент матрицы А + А Следствие 2. В графе (орграфе) тогда и только тогда существует цикл (контур), содержащий вершину vi, когда элемент (i, i) матрицы А + А Согласно следствию 1 в графе рис.3.13 для любой вершины существует путь в другую его вершину, т.к. матрица А + А Легко заметить, что матрица А На рис.3.14 показан орграф и его матрица смежности А.
Рис. 3.14 Матрицы А A Элемент a Матрица орграфа рис.3.14 А + А Определение: Маршрут в графе G=(V,E) есть чередующаяся последовательности вершин и ребер v0e1v1e2v2 …….vn-1envn графа G, для которой каждое ребро принадлежит двум соседним вершинам. При этом v0 – начало маршрута, vn – конец, n – длина маршрута. Обозначается через [u,v] маршрут между вершинами u и v. Иногда маршрут отмечен только вершинами, иногда только ребрами. Маршрут нулевой длины состоит из единственной вершины. Определение: Цепь в графе G есть маршрут без повторов ребер, возможны повторы вершин. Простая цепь в графе G есть цепь без повторов вершин, а следовательно и ребер. Определение: Цикл в графе G, есть замкнутая цепь (в которой начало и конец одинаковы). Простой цикл не имеет повторов вершин (кроме начала и конца), а следовательно, и повторов ребер. Замечание: цепь, простая цепь, цикл, простой цикл – есть некоторые подграфы в графе G. Замечание: В Орграфе маршрут, цепь, цикл становятся ориентированными. Определение: Контур есть ориентированный цикл.
|

 , где любые два "соседа" инцидентны.
, где любые два "соседа" инцидентны. - граф и, как обычно,
- граф и, как обычно,  .
.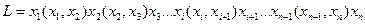 ,
, . Таким образом, среди вершин
. Таким образом, среди вершин  и ребер
и ребер 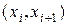 могут быть повторы. По символу пути на графической интерпретации графа можно воспроизвести «движение» от вершине к вершине, выбирая каждый раз очередное ребро в соот-ветствии с указанием в пути.
могут быть повторы. По символу пути на графической интерпретации графа можно воспроизвести «движение» от вершине к вершине, выбирая каждый раз очередное ребро в соот-ветствии с указанием в пути.
 v
v 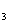 – простая цепь длиной 3, путь v1 x1 v2 x3 v4 x4 v3 x2 v2 x
– простая цепь длиной 3, путь v1 x1 v2 x3 v4 x4 v3 x2 v2 x 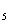 v
v  v
v  – цикл (не является простым), путь v2 x2 v3 x4 v4 x3 v2 – простой цикл.
– цикл (не является простым), путь v2 x2 v3 x4 v4 x3 v2 – простой цикл. матрицы А
матрицы А  равен числу всех путей длиной k из вершины v
равен числу всех путей длиной k из вершины v  в вершину v
в вершину v  , где А
, где А 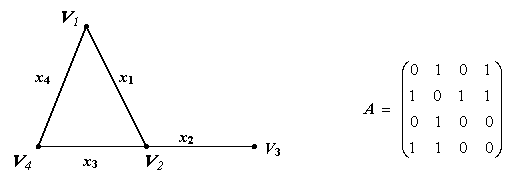
 и А
и А  для данного графа имеют вид:
для данного графа имеют вид: , A
, A  .
. матрицы А
матрицы А 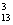 матрицы А
матрицы А  = 3.
= 3.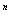 имела хотя бы один ненулевой диагональный элемент.
имела хотя бы один ненулевой диагональный элемент.
 , A
, A 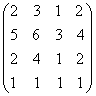 .
. = 5.
= 5.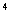 имеет ненулевые диагональные элементы, следовательно, согласно утверждению 4, он имеет хотя бы один контур. Это будет например, замкнутый путь v1 x2 v2 x7 v4 x8 v1.
имеет ненулевые диагональные элементы, следовательно, согласно утверждению 4, он имеет хотя бы один контур. Это будет например, замкнутый путь v1 x2 v2 x7 v4 x8 v1.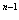 не равен нулю, где n – число вершин графа.
не равен нулю, где n – число вершин графа.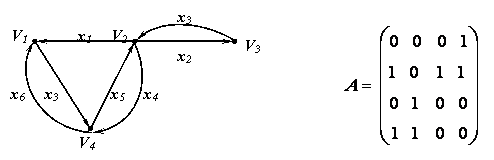
 , A
, A 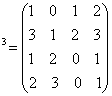 .
.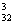 матрицы А
матрицы А  . Она не содержит нулевых элементов. Поэтому, по следствию 2 для любой вершины данного орграфа можно указать контур в который входит данная вершина.
. Она не содержит нулевых элементов. Поэтому, по следствию 2 для любой вершины данного орграфа можно указать контур в который входит данная вершина.


