Эйлеровы графы, цепи и циклы. Условия существования эйлерова цикла. Задача о разбиении графа на минимальное число цепей.
Цикл в графе называется эйлеровым, если он проходит через каждое ребро графа ровно один раз. Граф называется эйлеровым, если в нем есть эйлеров цикл. Теорема. Граф является эйлеровым тогда и только тогда, когда граф связный и все вершины имеют четную степень. Теорема. Ориентированный граф является эйлеровым тогда и только тогда, когда он сильно связный и для любой его вершины имеет место равенство: Свое название эйлеровы графы получили в честь Л.Эйлера, который первым рассмотрел такие графы в 1736 году в своей знаменитой работе о кенигсбергских мостах. Этой работой Эйлер, по существу, положил начало новому разделу математики - теории графов. Задача о кенигсбергских мостах состояла в следующем. На реке Прегель в Кенигсберге было два острова, соединенных между собой и с берегами семью мостами, как показано на рисунке:
Спрашивается, можно ли, начиная с некоторого места суши, обойти все мосты ровно по одному разу и вернуться в начальную точку? Эйлер предложил рассмотреть следующий граф:
Нетрудно догадаться, что решение этой задачи сводится к поиску эйлеровой цепи в данном графе. Однако, как показывает приведенная теорема, в указанном графе нет эйлеровых цепей. Эйлеровы цепи и циклы
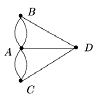
Классической в теории графов является следующая задача. В городе Кенигсберге имеется два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рисунке 36. Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя по одному разу по каждому мосту, вернуться обратно. Решение этой задачи сводится к нахождению некоторого специального маршрута в графе. Пусть G – псевдограф. Определение. Цепь (цикл) в G называется эйлеровой (эйлеровым), если она (он) проходит по одному разу через каждое ребро псевдографа G.
Поставим в соответствие схеме мультиграф G, изображенный на рисунке 37, в котором каждой части суши соответствует вершина, а каждому мосту – ребро, соединяющее соответствующие вершины. На языке теории графов задача звучит следующим образом: найти эйлеров цикл в мультиграфе G. Определение. Граф является эйлеровы м, если он содержит эйлеров цикл. Пусть
А вот пример графа, не являющегося эйлеровым:
Существует теорема (теорема Эйлера), полностью описывающая эйлеровы графы: граф является эйлеровым тогда и только тогда, когда он связен и все его локальные степени четны. Таким образом, имеется конкретный способ устанавливать, является или нет данный граф эйлеровым. Однако, если граф окажется эйлеровым, то указать его эйлеров цикл можно только после дополнительных исследований. В связи с эйлеровыми графами имеется одна классическая задача о минимальном цепном разбиении. Вот ее формулировка. Пусть В последней ситуации, указанной в этой формулировке, речь идет, очевидно, об эйлеро-вом графе. В первой же ситуации имеет смысл остановится на принципиальной схеме рассуж-дений. А именно: построим новый граф заметим, что полученный граф осуществим обход по циклу
Рассмотрим вопрос о наличии эйлеровой цепи и цикла в псевдографе. Теорема. Связный граф является эйлеровым тогда и только тогда, когда каждая вершина имеет четную локальную степень. Теорема. Связный граф содержит эйлерову цепь тогда и только тогда, когда ровно две вершины имеют нечетную локальную степень. Завершая рассмотрение эйлеровых графов, рассмотрим алгоритм построения эйлеровой цепи в данном эйлеровом графе. Этот метод известен под названием алгоритма Флёри. Теорема. Пусть G – эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графаG. Выходя из произвольной вершины и, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила: стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются; · на каждом этапе идем по мосту только тогда, когда нет других возможностей. Пример 84. Любой простой полный граф с нечетным количеством вершин является эйлеровым. Любой циклический граф является эйлеровым. Граф, являющийся колесом, не является эйлеровым. Определение. Пусть G – псевдограф. Тогда цикл (цепь) в G называется эйлеровым (эйлеровой), если он (она) проходит по одному разу через каждую дугу G, а псевдограф, содержащий эйлеров цикл, называется эйлеровым. Примером эйлерова графа являются так называемые сабли Магомета рис.3.21. Для этого графа замкнутый путь из первой вершины x
Рис.3.21 Как граф с эйлеровым циклом можно рассматривать, например, разумную схему обхода выставки так, чтобы увидеть каждый экспонат по одному разу. Теорема. (Критерий эйлеровости графа). Для того чтобы конечный связный граф был эйлеровым, необходимо и достаточно, чтобы степени всех его вершин были четными числами. Необходимость очевидна, т.к. двигаясь по эйлерову циклу, войдя в вершину по одной дуге, мы выходим из нее по другой дуге, т.е. каждой дуге “входа” соответствует дуга “выхода“. Каждая такая пара дуг дает вклад, равный двум, в степень вершины, а поскольку эйлеров цикл содержит все дуги, то степень каждой вершины представлена суммой двоек, и значит четна. На рис.3.22 графы G
Рис.3.22 Граф рис. 3.4 является связным, но не эйлеровым, т.к. степени всех его вершин нечетные числа. Следовательно, задача о Кенигсбергских мостах не имеет решения. Теорема. Пусть G – конечный связный орграф. Для того, чтобы существовал ориентированный цикл в G, содержащий все дуги (эйлеров цикл), необходимо и достаточно, чтобы в каждой вершине орграфа число входящих и выходящих дуг было одинаково. На рис3.23 изображен орграф для которого выполняются условия этой теоремы. Для него ориентированный цикл x
Рис. 3.23 Определение. Связный граф называется квазиэйлеровым, если на нем существует эйлерова цепь. Теорема. (Критерий квазиэйлеровости). Для того чтобы конечный связный граф был квазиэйлеровым, необходимо и достаточно, чтобы степени всех его вершин были четными числами или степени всех его вершин, за исключением ровно двух, были четными числами, причем в первом случае эйлерова цепь является эйлеровым циклом, а во втором случае эйлерова цепь начинается в одной из вершин нечетной степени, а заканчивается в другой вершине нечетной степени. Данная теорема является следствием предыдущей. Случай двух вершин нечетной степени и построение эйлеровой цепи можно свести к эйлерову циклу на графе, полученному из данного добавлением дуги, соединяющей две вершины нечетной степени Из рис.3.22 видно, что связные графы G
|

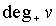 =
=  .
.

 - граф. Эйлеровым циклом в графе называется такой цикл, который содержит все ребра и все вершины этого графа. Напомним, что, по определению, в циклах не повторяются ребра. Таким образом, при наличии эйлерова цикла в графе этот граф можно обойти по всем ребрам, пройдя каждое ребро только один раз. Граф, обладающий эйлеровым циклом, сам называется эйлеровым.
- граф. Эйлеровым циклом в графе называется такой цикл, который содержит все ребра и все вершины этого графа. Напомним, что, по определению, в циклах не повторяются ребра. Таким образом, при наличии эйлерова цикла в графе этот граф можно обойти по всем ребрам, пройдя каждое ребро только один раз. Граф, обладающий эйлеровым циклом, сам называется эйлеровым. Вот пример эйлерова графа:
Вот пример эйлерова графа:
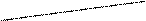




 - все его вершины нечетной степени (на-помним, что в каждом графе число вершин нечетной степени четно). Тогда, если
- все его вершины нечетной степени (на-помним, что в каждом графе число вершин нечетной степени четно). Тогда, если 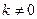 , то минимальное число цепей графа, содержащих в совокупности все его ребра, равно
, то минимальное число цепей графа, содержащих в совокупности все его ребра, равно  ; если же
; если же  , то указанное минимальное число равно 1.
, то указанное минимальное число равно 1. , в котором
, в котором  (т.е. добавляется одна новая вершина) и
(т.е. добавляется одна новая вершина) и  (т.е. добавляется еще
(т.е. добавляется еще 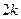 ребер);
ребер); ;
;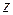 ; те
; те 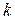 цепей, о которых идет речь в обсуждаемом утверждении, будут выделяться в процессе этого обхода так: обход начинается в вершине
цепей, о которых идет речь в обсуждаемом утверждении, будут выделяться в процессе этого обхода так: обход начинается в вершине 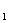 x
x 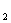 x
x 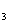 x
x  x
x 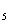 x
x  будет эйлеровым циклом.
будет эйлеровым циклом.

 является эйлеровым.
является эйлеровым.



