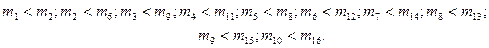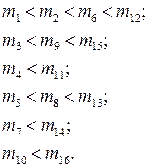Пусть 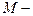 частично упорядоченное множество (сокращенно: ЧУМ). Это значит, что задано некоторое подмножество
частично упорядоченное множество (сокращенно: ЧУМ). Это значит, что задано некоторое подмножество 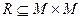 такое, что выполнены следующие условия: для всякого
такое, что выполнены следующие условия: для всякого 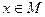 обязательно
обязательно 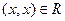 (это, так называемая, рефлексивность); если
(это, так называемая, рефлексивность); если 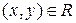 и
и 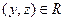 , то обязательно
, то обязательно 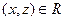 (это, так называемая, транзитивность); если
(это, так называемая, транзитивность); если 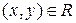 и
и 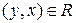 , то обязательно
, то обязательно 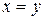 (это, так называемая, антисимметричность). Само множество
(это, так называемая, антисимметричность). Само множество 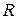 называется частичным порядком. На одном и том же множестве
называется частичным порядком. На одном и том же множестве 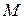 может быть много частичных порядков.
может быть много частичных порядков.
Если частичный порядок 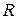 таков, что для любых двух элементов
таков, что для любых двух элементов  либо
либо 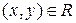 либо
либо 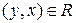 , то говорят, что множество
, то говорят, что множество 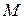 является цепью; если же частичный порядок
является цепью; если же частичный порядок 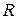 таков, что для любых различных
таков, что для любых различных  ни одно из включений -
ни одно из включений - 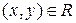 ,
, 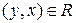 - не выполняется, то говорят, что
- не выполняется, то говорят, что 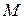 является антицепью. Очевидно, что если
является антицепью. Очевидно, что если 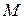 - ЧУМ, то и любое подмножество в
- ЧУМ, то и любое подмножество в 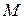 является частично-упорядоченным. По определению по-лагают, что всякое одноэлементное подмножество является одновременно и цепью и анти-цепью.
является частично-упорядоченным. По определению по-лагают, что всякое одноэлементное подмножество является одновременно и цепью и анти-цепью.
Рассмотрим пример. Пусть 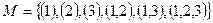 (это означает, что элемента-ми множества
(это означает, что элемента-ми множества 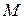 являются наборы указанных натуральных чисел). Определим частичный по-рядок
являются наборы указанных натуральных чисел). Определим частичный по-рядок 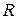 , объявив, что
, объявив, что 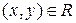 , если
, если 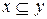 . Нетрудно проверить, что это - действительно частичный порядоок. В этом частичном порядке
. Нетрудно проверить, что это - действительно частичный порядоок. В этом частичном порядке 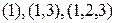 - цепь, а
- цепь, а 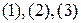 - анти-цепь.
- анти-цепь.
Существует классическая задача: разбить ЧУМ 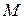 на минимальное число цепей. Это значит надо найти в
на минимальное число цепей. Это значит надо найти в 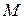 цепи
цепи 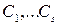 такие, что у любых двух из них нет общих элементов, что их объединение совпадает с
такие, что у любых двух из них нет общих элементов, что их объединение совпадает с 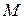 и при всем при этом число
и при всем при этом число  минимально возможное. Имеется по этому поводу классическая теорема Дилворта, утверждающая следующее:
минимально возможное. Имеется по этому поводу классическая теорема Дилворта, утверждающая следующее:
минимальное число цепей, на которые можно разбить данное частично упорядоченное множество, равно максимальному числу элементов, составляющих антицепь.
Мы приведем сейчас алгоритм, позволяющий отыскать одно из возможных минималь-ных цепных разбиений ЧУМа, т.е. найти набор попарно неперсекающихся цепей 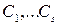 , объ-единение которых совпадает с
, объ-единение которых совпадает с 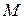 и при этом
и при этом  миниально возможное.
миниально возможное.
Для удобства мы будем в будущем выражать тот факт, что 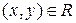 в ЧУМе
в ЧУМе 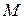 сим-волом
сим-волом 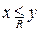 или просто
или просто 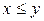 , причем если к тому же
, причем если к тому же 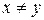 , то будем писать
, то будем писать  .
.
Итак, пусть 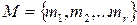 - ЧУМ; требуется найти минимальное цепное разбиение.
- ЧУМ; требуется найти минимальное цепное разбиение.
Шаг 0. Построим двудольный граф 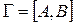 следующим образом. Положим
следующим образом. Положим 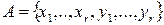 ; это означает, что в графе будет ровно
; это означает, что в графе будет ровно 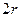 вершин. Далее, ребра в графе будут иметь лишь следующий вид:
вершин. Далее, ребра в графе будут иметь лишь следующий вид: 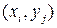 , причем
, причем 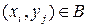 тогда и только тогда, когда
тогда и только тогда, когда 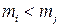 .
.
Шаг 1. Выберем в построенном графе G наибольшее паросочетание 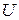 . Для каждого ребра
. Для каждого ребра 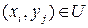 фиксируем пару элементов
фиксируем пару элементов 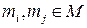 , составляющих, естественно, цепь, так как по определению ребер в G обязательно
, составляющих, естественно, цепь, так как по определению ребер в G обязательно 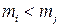 .
.
Шаг 2. Многократно используя свойство транзитивности частичного порядка, объеди-ним двухэлементные цепи из предыдущего шага в неудлиняемые цепи. В результате получится некоторый набор цепей 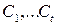 в данном множестве, причем, как нетрудно проверить, эти це-пи попарно общих элементов не имеют. Добавив к этому списку цепей одноэлементные цепи, полученные из всех элементов данного множества, не вошедших в объединение
в данном множестве, причем, как нетрудно проверить, эти це-пи попарно общих элементов не имеют. Добавив к этому списку цепей одноэлементные цепи, полученные из всех элементов данного множества, не вошедших в объединение 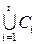 , мы получим некоторое цепное разбиение данного множества
, мы получим некоторое цепное разбиение данного множества 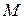 . Можно доказать, что это цепное разбиение минимально.
. Можно доказать, что это цепное разбиение минимально.
ПРИМЕР. Пусть множество 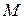 состоит из следующих наборов чисел (каждый набор заключен в круглые скобки):
состоит из следующих наборов чисел (каждый набор заключен в круглые скобки):
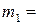 Æ (пустое множество; это - тоже лемент из
Æ (пустое множество; это - тоже лемент из 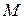 );
);
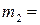 (1),
(1), 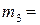 (2),
(2), 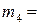 (3),
(3), 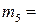 (4),
(4), 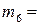 (1,2),
(1,2), 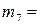 (1,3),
(1,3), 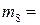 (1,4),
(1,4), 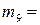 (2,3),
(2,3), 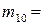 (2,4),
(2,4), 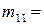 (3,4),
(3,4),  (1,2,3),
(1,2,3), 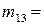 (1,2,4),
(1,2,4),  (1,3,4),
(1,3,4), 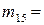 (2,3,4),
(2,3,4), 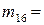 (1,2,3,4).
(1,2,3,4).
Частичный порядок на 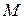 будет считаться по включению:
будет считаться по включению: 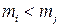 тогда и только тог-да, когда
тогда и только тог-да, когда 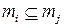 .
.
Найдем минимальное цепное разбиение этого множества. Вначале построим двудольный граф для данной задачи. Вот его матрица:
Найдем наибольшее паросочетание:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| х
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| х
| х
| х
| х
| х
|
|
|
| х
| х
| х
|
|
|
| х
|
|
|
|
| х
| х
| х
| х
| х
|
| х
| х
|
|
| х
|
|
| х
|
|
|
|
|
| х
| х
| х
| х
| х
| х
|
| х
|
| х
|
|
| х
|
|
|
|
|
|
| х
| х
| х
| х
| х
| х
| х
|
| х
|
|
| х
|
|
|
|
|
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
|
| х
| х
|
|
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| х
|
| х
|
|
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
|
| х
|
|
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| х
| х
|
|
|
|
| 10 11110
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| х
|
|
|
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
|
|
| -
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| -
|
|
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| -
|
| 14 4
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| -
|
| 15 5
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
|
| -
|
| 16 6
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| х
| -
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, наибольшее паросочетание таково:
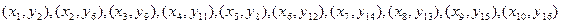 .
.
Отсюда - первые «двуэлементные цепочки»:
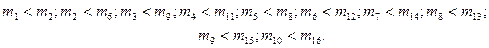
Используя транзитивность частичного порядка, склеим некоторые из этих цепочек:
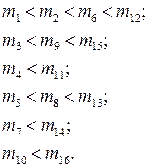
Поскольку не осталось элементов данного множества вне указанных цепей, этот набор цепей и является минимальным цепным разбиением.

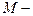 частично упорядоченное множество (сокращенно: ЧУМ). Это значит, что задано некоторое подмножество
частично упорядоченное множество (сокращенно: ЧУМ). Это значит, что задано некоторое подмножество 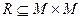 такое, что выполнены следующие условия: для всякого
такое, что выполнены следующие условия: для всякого 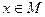 обязательно
обязательно 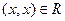 (это, так называемая, рефлексивность); если
(это, так называемая, рефлексивность); если 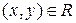 и
и 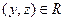 , то обязательно
, то обязательно 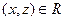 (это, так называемая, транзитивность); если
(это, так называемая, транзитивность); если 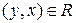 , то обязательно
, то обязательно 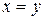 (это, так называемая, антисимметричность). Само множество
(это, так называемая, антисимметричность). Само множество 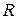 называется частичным порядком. На одном и том же множестве
называется частичным порядком. На одном и том же множестве 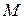 может быть много частичных порядков.
может быть много частичных порядков. либо
либо 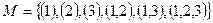 (это означает, что элемента-ми множества
(это означает, что элемента-ми множества 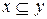 . Нетрудно проверить, что это - действительно частичный порядоок. В этом частичном порядке
. Нетрудно проверить, что это - действительно частичный порядоок. В этом частичном порядке 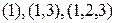 - цепь, а
- цепь, а 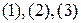 - анти-цепь.
- анти-цепь.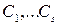 такие, что у любых двух из них нет общих элементов, что их объединение совпадает с
такие, что у любых двух из них нет общих элементов, что их объединение совпадает с  минимально возможное. Имеется по этому поводу классическая теорема Дилворта, утверждающая следующее:
минимально возможное. Имеется по этому поводу классическая теорема Дилворта, утверждающая следующее: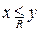 или просто
или просто 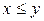 , причем если к тому же
, причем если к тому же 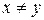 , то будем писать
, то будем писать  .
.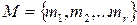 - ЧУМ; требуется найти минимальное цепное разбиение.
- ЧУМ; требуется найти минимальное цепное разбиение.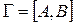 следующим образом. Положим
следующим образом. Положим 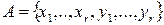 ; это означает, что в графе будет ровно
; это означает, что в графе будет ровно 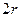 вершин. Далее, ребра в графе будут иметь лишь следующий вид:
вершин. Далее, ребра в графе будут иметь лишь следующий вид: 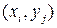 , причем
, причем 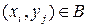 тогда и только тогда, когда
тогда и только тогда, когда 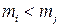 .
.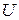 . Для каждого ребра
. Для каждого ребра 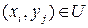 фиксируем пару элементов
фиксируем пару элементов 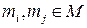 , составляющих, естественно, цепь, так как по определению ребер в G обязательно
, составляющих, естественно, цепь, так как по определению ребер в G обязательно 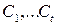 в данном множестве, причем, как нетрудно проверить, эти це-пи попарно общих элементов не имеют. Добавив к этому списку цепей одноэлементные цепи, полученные из всех элементов данного множества, не вошедших в объединение
в данном множестве, причем, как нетрудно проверить, эти це-пи попарно общих элементов не имеют. Добавив к этому списку цепей одноэлементные цепи, полученные из всех элементов данного множества, не вошедших в объединение 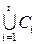 , мы получим некоторое цепное разбиение данного множества
, мы получим некоторое цепное разбиение данного множества 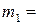 Æ (пустое множество; это - тоже лемент из
Æ (пустое множество; это - тоже лемент из 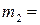 (1),
(1), 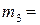 (2),
(2), 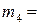 (3),
(3), 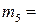 (4),
(4), 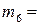 (1,2),
(1,2), 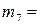 (1,3),
(1,3), 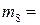 (1,4),
(1,4), 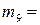 (2,3),
(2,3), 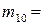 (2,4),
(2,4), 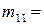 (3,4),
(3,4),  (1,2,3),
(1,2,3), 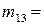 (1,2,4),
(1,2,4),  (1,3,4),
(1,3,4), 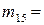 (2,3,4),
(2,3,4), 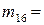 (1,2,3,4).
(1,2,3,4).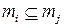 .
.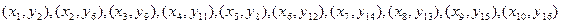 .
.