Понятие связности. Компоненты связности.
Вершины
a 5
вершины a 3 и a 5 связаны (путем Граф, в котором связанны любые две вершины, называется связным. Таким образом, выше приведен пример графа несвязного. Связной компонентой графа называется такой его подграф, который является сам по себе графом связным и при этом совпадающим с любым другим содержащим его связным подграфом. Таким образом, связный граф обладает единст-венной связной компонентой - это он сам. А вот приер графа с тремя связными компонетами (имена вершин не имеют значения):
Вот схематическое изображение простого цикла:
А вот схематическое изображение цикла, не являющегося простым:
Две вершины Орграф называется связным, если в нем любые две вершины связаны. Определение: Граф (Орграф) G связен, если любая пара его вершин u,v может быть соединена цепью (путем) от u к v. В противном случае, граф G несвязен. Компонента связности графа G есть наибольший по числу ребер связный подграф графа G. Определение. Граф (орграф) называется связным (сильно связным), если для любых двух его вершин vi и vj существует путь из вершины vi в вершину vj. Определение. Граф называется связным, если для любых двух его вершин v, w существует простая цепь из v в w. Определение. Граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v, w (из v и w). Определение. Орграф называется односторонне связным, если для любых двух его вершин, по крайней мере, одна достижима из другой.
Псевдографом, ассоциированным с ориентированным псевдографом, называется псевдограф, получающийся из ориентированного псевдографа, путем замены направленных дуг на дуги без стрелок. На рис. 3.17 показан односторонне связный ориентированный псевдограф и ассоциированный с ним псевдограф.
Рис. 3.17 Определение. Орграф, не являющийся сильно связным, называется слабо связным, если связным является ассоциированный с ним граф. Орграф рис.3.17 является слабо связным.
|

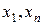 в приведенных выше обозначениях называются концами пути и связан-ными или соединенными путем L. Отдельным термином выделяют тот факт, что две вершины графа могут быть связаны некоторым путем: их называют связанными. Например, в графе
в приведенных выше обозначениях называются концами пути и связан-ными или соединенными путем L. Отдельным термином выделяют тот факт, что две вершины графа могут быть связаны некоторым путем: их называют связанными. Например, в графе
 a 1
a 1
 a 2 a 3. a 4
a 2 a 3. a 4 ), а вершины a 4 и a 1 нет.
), а вершины a 4 и a 1 нет.







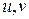 орграфа называются связанными, если имеется орпуть из
орграфа называются связанными, если имеется орпуть из 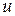 в
в  и одновременно имеется орпуть из
и одновременно имеется орпуть из 



