Гамильтоновы графы, цепи и циклы. Условия Дирака, Оре и Поша, гарантирующие существование в графе гамильтонова цикла.
Пусть G – псевдограф. Определение. Цепь (цикл) в G называется гамильтоновой (гамильтоновыми), если она (он) проходит по одному разу через каждую вершину псевдографа G. Определение. Граф является гамильтоновым, если он содержит гамильтонов цикл. С понятием гамильтоновых циклов тесно связана так называемая задача коммивояжера: в нагруженном графе G определить гамильтонов цикл минимальной длины (иными словами, коммерсант должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, и при этом стоимость такой поездки должна быть минимальной). Приведем теорему Дирака, которая отвечает на вопрос: существует ли в графе гамильтонов цикл. Теорема. Если в простом графе с n (і 3) вершинами локальная степень каждой вершины не менее n/2, то граф является гамильтоновым. Пример 85. Любой простой полный граф является гамильтоновым. Любой циклический граф является гамильтоновым. Граф, являющийся колесом, является гамильтоновым. Цикл в графе называется гамильтоновым, если он проходит через каждую вершину графа ровно один раз. Граф называется гамильтоновым, если в нем есть гамильтонов цикл. Указанные названия циклов связаны с именем Уильяма Гамильтона, который в 1859 году предложил следующую игру головоломку. Требуется, переходя по очереди от одной вершины додекаэдра к другой вершине по его ребру, обойти все 20 вершин по одному разу и вернуться в начальную вершину. Отметим, что придумано еще много других развлекательных и полезных задач, связанных с поиском гамильтоновых циклов. Сформулируем две из них: 1. Кампанию из нескольких человек требуется рассадить за круглым столом таким образом, чтобы по обе стороны от каждого сидели его знакомые. Очевидно, для решения этой задачи нужно найти гамильтонов цикл в графе знакомств компании. 2. (Задача о шахматном коне.) Можно ли, начиная с произвольного поля шахматной доски, обойти конем последовательно все 64 поля по одному разу и вернуться в исходное поле? Несмотря на внешнее сходство задач об эйлеровых и гамильтоновых циклах, оказалось, что эффективных критериев существования гамильтоновых циклов (в отличии от эйлеровых) не существует. Определение. Цикл (цепь) в псевдографе называется гамильтоновым (гамильтоновой ), если он (она) проходит через каждую вершину псевдографа ровно один раз. Длина любой гамильтоновой цепи равна (n-1), а длина любого гамильтонового цикла равна n – число вершин псевдографа. С понятием гамильтоновых циклов связана так называемая задача о коммивояжере: в нагруженном графе надо определить гамильтонов цикл минимальной длины. Иными словами, коммерсант должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, и при этом стоимость поездки должна быть минимальной. Задача о коммивояжере имеет ряд приложений в исследовании операций, например в вопросах о наиболее эффективном использовании подвижного состава или оборудования. Задача может быть решена перебором, а в общем случае никакого эффективного алгоритма решения нет. Имеются некоторые частные схемы для отдельных случаев. Критерия для существования гамильтоновых циклов не известно. Более того, иногда даже для конкретных графов бывает трудно решить, можно ли найти такой цикл. Утверждение. В полном графе всегда существует гамильтонов цикл, а также гамильтоновы цепи, соединяющие две произвольные вершины этого графа. Т.о. простейшим достаточным условием существования гамильтоновых цепей и циклов в графе является его полнота. Необходимым условием существования гамильтоновых цепей и циклов является связность графа. Теорема. Если в графе с n вершинами для любых двух различных несмежных вершин v i и v j графа выполняется условие deg v i + deg v j e n, (3.6) то в графе существует гамильтонов цикл. Если выполняется условие dеgv то в графе существует гамильтонова цепь. Следствие. Если для любой вершины v графа выполняется условие degv e n/2, то в графе существует гамильтонов цикл. Из рис.3.22 видно, что для графа G Для графа G Для графа G Эйлеровы и гамильтоновы циклы не являются эквивалентными понятиями. Это видно из рис. 3.22. Для графа G1 есть оба цикла, для графа G2 есть эйлеров цикл, но нет гамильтонова, для графа G3 есть гамильтонов цикл, но нет эйлерова, а для графа G
Гамильтонов цикл и гамильтонов граф. Условия Дирака, Оре и Поша, гарантирующие существование в графе гамильтонова цикла. Пусть
Общих и легко осуществляемых действий, с помощью которых можно было бы достоверно выяснить, является ли данный граф гамильтоновым, не существует. Однако, имеются доста-точные условия на гамильтоновость, которые проверятются легко. Недостаток здесь состоит в том, что даже если ни одно из этих условий не выполняется, граф может оказаться гамильто-новым. В дальнейшем в этой лекции будет молчаливо предполагаться, что число вершин в лю-бом рассматриваемом графе не меньше трех. Итак, условие первое - условие Дирака. Пусть Вот пример графа Дирака:
Очевидно, этот граф - гамильтонов. А вот пример гамильтонова графа, не являющегося графом Дирака:
Условие второе - условие Оре. По-прежнему будем обозначать через Вот пример графа Оре:
А вот пример графа, не являющегося графом Оре и, тем не менее, графа гамильтонова:
Нетрудно заметить, что всякий граф Дирака автоматически является графом Оре. Но вот пример графа Оре, не являющегося графом Дирака:
Условие третье - условие Поша. Это - более сложная конструкция. Введем следующую функцию для которого и строится функция
написанное означает, что функция Для примера построим функцию Поша следующего графа:
Функция будет описано таблично:
Теперь сформулируем условие Поша. Графом Поша называется граф 1) для 2) если Можно доказать, что каждый граф Поша обязательно гамильтонов. Легко заметить, что простой цикл на большом числе вершин графом Поша не является, но, конечно, явяляется га-мильтоновым графом. Кроме того, нетрудно заметить, что всякий граф Дирака является графом Поша. То же верно и в отношении графов Оре: каждый граф Оре является графом Поша. Обратное в обоих последних случаях неверно. Вот пример: фиксируем какой-нибудь полный граф на достаточно большом числе вершин; добавим к нему еще одну вершину и соединим ее с любыми двумя вершинами в исходном графе; очевидно, вновь полученный граф - гамильтонов; фиксируем в нем какой-нибудь гамильтонов цикл и удалим из графа какое-нибудь ребро, не включенное в этот цикл; полученный в результате граф будет, как нетрудно проверить, графом Поша; однако, он не будет графом Оре - будут сразу две пары несмежных вершин, сумма степеней которых меньше числа вершин в графе. Самостоятельная работа № 5. (см. Приложение).
|

 + degv
+ degv  e n – 1, (3.7)
e n – 1, (3.7) оба условия теоремы не выполняются, поэтому граф G
оба условия теоремы не выполняются, поэтому граф G  оба условия теоремы выполняются, поэтому он имеет гамильтонов цикл и гамильтоновы цепи.
оба условия теоремы выполняются, поэтому он имеет гамильтонов цикл и гамильтоновы цепи. условие (3.7) выполняется, а условие (3.6) нет, поэтому граф G
условие (3.7) выполняется, а условие (3.6) нет, поэтому граф G 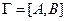 - некоторый граф. Он называется гамильтоновым,если в нем сущест-вует простой цикл, содержащий все вершины графа. Например, каждый полный граф – гамиль-тонов, потому что в нем проведены всевозможные ребра и, в частности, те, благодаря которым возможен обход по всем вершинам. А вот пример графа, не являющегося гамильтоновым:
- некоторый граф. Он называется гамильтоновым,если в нем сущест-вует простой цикл, содержащий все вершины графа. Например, каждый полный граф – гамиль-тонов, потому что в нем проведены всевозможные ребра и, в частности, те, благодаря которым возможен обход по всем вершинам. А вот пример графа, не являющегося гамильтоновым:


 - число вершин в данном графе; если степень каждой вершины не меньше, чем
- число вершин в данном графе; если степень каждой вершины не меньше, чем 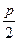 , то граф называется графом Дирака. Можно дока-зать, что каждый граф Дирака обязательно гамильтонов.
, то граф называется графом Дирака. Можно дока-зать, что каждый граф Дирака обязательно гамильтонов.











 выполнено неравенство
выполнено неравенство  , то граф называвается графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Можно доказать, что всякий граф Оре обяза-тельно гамильтонов.
, то граф называвается графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Можно доказать, что всякий граф Оре обяза-тельно гамильтонов.






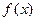 целого неотрицательного аргумента
целого неотрицательного аргумента  . Сначала запишем определение формулой, а затем прокомментируем его. Итак, речь идет по-прежнему о графе
. Сначала запишем определение формулой, а затем прокомментируем его. Итак, речь идет по-прежнему о графе  ;
;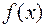 в каждом целом неотрицательном
в каждом целом неотрицательном 
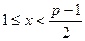 выполняется неравенство
выполняется неравенство  ;
;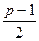 - целое число, то при
- целое число, то при  имеет место неравенство:
имеет место неравенство: 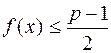 .
.


