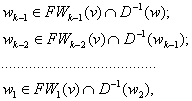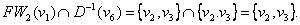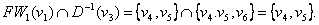Поиск путей в графах и минимальных путей в орграфах
Определение. Матрицей связности графа G называется квадратная матрица S (G) порядка n, у которой s ij = 1, если i = j или существует путь, соединяющий v i и v j, и s ij = 0 – в противном случае. Матрицу связности графа (орграфа) можно вычислить по следующей формуле: S (G) = sign(E + A + A где E – единичная матрица, A – матрица смежности графа. Определение. Матрицей достижимости орграфа G называется квадратная матрица T (G) порядка n, у которой t Определение. Матрицей сильной связности орграфа G называется квадратная матрица S (G) порядка n, у которой s ij = 1, если вершина v i достижима из вершины v j и одновременно v j достижима из v i, и s ij = 0 – в противном случае. Матрицу достижимости и матрицу сильной связности орграфа можно вычислить по следующим формулам: T (G) = sign (E + A + A S (G) = T (G) T (G) где т – операция транспонирования, A – матрица смежности орграфа. В матрице связности (сильной связности) графа (орграфа), элемент отличен от нуля тогда и только тогда, когда соответствующие вершины принадлежат одной компоненте связности (сильной связности). При решении некоторых прикладных задач нередко возникает необходимость найти путь, соединяющий заданные вершины графа. Рассмотрим алгоритм (Тэрри) поиска пути в связном графе, из вершины v i в вершину v j, где v i Исходя из вершины v i осуществлять последовательный переход от каждой достигнутой вершины к смежной ей вершине, по следующим правилам: 1. идя по произвольной дуге, всякий раз отмечать направление, в котором оно было пройдено; 2. исходя из некоторой вершины vk, всегда следовать только по дуге, которое не было пройдено или было пройдено в противоположном направлении; 3. для всякой вершины vk, отличной от v i, отмечать первую заходящую в vk дугу, если вершина vk встречается в первый раз; 4. исходя из некоторой вершины, vk, отличной от вершины v i, по первой заходящей в vk дуге идти лишь тогда, когда нет других возможностей. Пример. Используя алгоритм Тэрри, найти путь из вершины v1 в вершину v5 в графе, изображенном на рис. 3.24.
Рис. 3.24 Поиск искомого пути будем осуществлять так, как будто мы ничего не знаем об этом графе. Например, что граф это схема лабиринта, а v5 это выход из него. На рис. 3.25 показан один из возможных вариантов движения по графу, согласно алгоритму Тэрри. Пронумерованными дугами показана схема движения. Знаками « Замечание. Из полученного с помощью данного алгоритма пути всегда можно выделить простую цепь, соединяющую вершины v i и v j. Для данного примера это будет v1 v3 v5.
Рис. 3.25 Часто возникает задача поиска путей в орграфе с минимальным числом дуг. Путь в орграфе из вершины v i в вершину v j, где v i ` v j, называется минимальным, если он имеет минимальную длину среди всех путей орграфа из v i в v j. Для минимальных путей справедливы следующие утверждения: 1) Любой минимальный путь является простой цепью; 2) Пусть v1 v2 … vk, где v1 ` vk – минимальный путь. Тогда для любых номеров i, j таких, что 1d i < j d k, путь v i vi+1 … vk также является минимальным. Пусть G(V, X) – орграф. Введем следующие обозначения. G(v i) = {v G G(V1) = v i G v i Рассмотрим алгоритм (алгоритм фронта волны) поиска минимального пути с n вершинами из вершины v i в вершину v j орграфа. Шаг1. Помечаем вершину v i индексом 0. Затем помечаем вершины, принадлежащие образу вершины v i, индексом 1. Множество вершин с индексом 1 обозначим FW1(v i). Полагаем k=1. Шаг2. Если FW Шаг3. Если v j Последовательность вершин v i v1 v2 … v v v ........................ v На этом работа алгоритма заканчивается. Шаг 4. Помечаем индексом k+1 все непомеченные вершины, которые при-надлежат образу множества вершин с индексом k. Множество вершин с индексом k + 1 обозначим FW Замечание 1. Множество FW Замечание 2. Вершины v1,…, vk-1 из (3.11), вообще говоря, могут быть выделены неоднозначно. Эта неоднозначность соответствует случаю, когда существует несколько различных путей из вершины v i в v j. Пример. Используя алгоритм фронта волны, определить минимальный путь из вершины v1 в вершину v6 в орграфе, заданном матрицей смежности, представленной табл.3.6. Таблица 3.6
Шаг 1. Помечаем v1 индексом 0, т.е. v1 Шаг 2. Т.к. FW1(v1) ` Ш, то переходим к шагу 3. Шаг 3. v6 Шаг 4. По табл.3.6 находим образ множества вершин, принадлежащих множеству FW1(v1). Это будет следующее множество {v2, v3, v5, v1, v4 }. Непомеченные вершины этого множества будут v2 и v3. Их помечаем индексом 2, т.е. v Шаг 2. Т.к. FW2(v1) ` Ш, то переходим к шагу 3. Шаг 3. v6 Шаг 4. По табл. 3.6 находим образ множества вершин, принадлежащих множеству FW2(v1). Это будет следующее множество {v1, v4, v5, v6, v2}. Непомеченных вершин в этом множестве только v6. Следовательно, FW3(v1) = v6. Переходим к шагу 2. Шаг 2. Т.к. FW3(v1) ` Ш следовательно, переходим к шагу 3. Шаг 3. v6 Определим следующее множество, используя первую строчку в (3.11). FW2(v1)) G-1(v6) = {v2, v3}) {v2, v3} = {v2, v3}. Выберем любую вершину из этого множества, например v3. Тогда определим следующее множество, используя вторую строчку в (3.11). FW1(v1)) G Выберем любую вершину из этого множества, например v5. Тогда искомый путь длины 3 из вершины v1 в вершину v6 будет следующим v1 v5 v3 v6. §6.4. Задачи поиска маршрутов (путей) в графе (орграфе) Поиск путей (маршрутов) с минимальным числом дуг (ребер) При решении некоторых прикладных задач нередко возникает необходимость найти маршрут, соединяющий заданные вершины в графе G. Данная задача решается при использовании алгоритма Тэрри. Рассмотрим более сложную задачу: нахождение пути (маршрута) с минимальным числом дуг (ребер). Определение.Путь в орграфе D из вершины v в вершину w, где v№w, называется кратчайшим, если он имеет минимальную длину среди всех путей орграфа D из v и w. Аналогично определяется и кратчайший маршрут в графеG. Утверждение. Любой кратчайший путь (маршрут) является простой цепью. Рассмотрим задачу поиска минимального пути (маршрута). Введем некоторые обозначения. Пусть D=(V, X) – орграф, vОV, V1МV. Обозначим D(v)={wОV| (v, w)ОX} – образ вершины v; D-1(v)={wОV| (w,v)ОX} – прообраз вершины v; Пусть D=(V, X) – орграф с n і 2 вершинами и v, w – заданные вершины из V, где v № w. Опишем алгоритм поиска кратчайшего пути из v в w в орграфе D. Алгоритм фронта волны. Шаг 1. Помечаем вершину v индексом 0. Затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначаем FW1(v). Полагаем k=1. Шаг 2. Если FWk(v)=Ж или выполняется k=n-1, wПFWk(v), то вершина w не достижима из v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3. Шаг 3. Если wПFWk(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k, и этот путь является кратчайшим. Последовательность вершин vw1w2…wk-1w, где
и есть искомый кратчайший путь из v и w. На этом работа алгоритма заканчивается. Шаг 4. Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k+1 обозначаем FWk+1(v). Присваиваем k:=k+1 и переходим к шагу 2. Замечание. Множество FWk(v) обычно называют фронтом волны k -го уровня. Замечание. Вершины w1w2…wk-1, вообще говоря, могут быть выделены неоднозначно. Эта неоднозначность соответствует случаям, когда существует несколько различных кратчайших путей из v и w. Пример 81. Определить кратчайший путь из v1 и v6 в орграфе D, заданном матрицей смежности (табл. 67). Таблица 67
Решение. Согласно алгоритму Фронта волны, последовательно определяем FW1(v1) = {v4, v5}; FW2(v1) = D(FW1(v1))\{v1, v4, v5} = {v2, v3}; FW3(v1) = D(FW2(v1))\{v1, v2, v3, v4, v5} = {v6}. Таким образом, v6 О FW3(v1), а значит, существует путь из v1 в v6 длины 3, и этот путь является кратчайшим. Найдем теперь кратчайший путь из v1 в v6. Определим множество
Выберем любую вершину из найденного множества, например вершину v3. Определим далее множество
Выберем любую вершину из найденного множества, например вершину v5. Тогда v1v5v3v6 – искомый кратчайший путь из v1 в v6 (длины 3) в орграфе D.
|

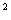 + … + A
+ … + A 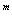 ), (3.8)
), (3.8)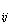 = 1, если вершина vj достижима из вершины vi и t ij = 0 – в противном случае.
= 1, если вершина vj достижима из вершины vi и t ij = 0 – в противном случае.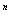 ), (3.9)
), (3.9)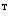 , (3.10)
, (3.10) v j.
v j.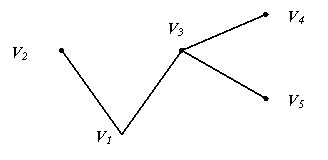
 » помечены первые заходящие в вершины графа дуги. Указанная на рис.3.25 схема движения, соответствует пути: v1 v2 v1 v3 v4 v3 v5.
» помечены первые заходящие в вершины графа дуги. Указанная на рис.3.25 схема движения, соответствует пути: v1 v2 v1 v3 v4 v3 v5.
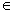 V | (vi,v)
V | (vi,v) 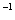 (v i) = {v
(v i) = {v  G(v i) – образ множества вершин орграфа V1
G(v i) – образ множества вершин орграфа V1 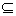 V.
V.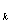 (v) = Ш или выполняется k = n – 1, v j
(v) = Ш или выполняется k = n – 1, v j 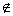 FW
FW 
 v j и есть минимальный путь из v i в v j. Вершины в этом пути определяются следующими соотношениями
v j и есть минимальный путь из v i в v j. Вершины в этом пути определяются следующими соотношениями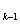
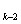
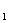
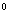 . По табл. 3.6 находим вершины, принадлежащие образу вершины v1. Это будут вершины v4 и v5. Их помечаем индексом 1, т.е. v4
. По табл. 3.6 находим вершины, принадлежащие образу вершины v1. Это будут вершины v4 и v5. Их помечаем индексом 1, т.е. v4  , v5
, v5  , v
, v 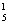 ). Полагаем k = 1.
). Полагаем k = 1.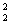 , v
, v 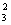 . Это множество обозначаем FW2 (v1) = {v
. Это множество обозначаем FW2 (v1) = {v 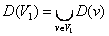 - образ множества вершин V1;
- образ множества вершин V1; 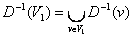 - прообраз множества вершин V1. Пусть G=(V, X) – граф, vОV, V1МV. Обозначим G(v)={wОV|{v, w}ОX} – образ вершины v;
- прообраз множества вершин V1. Пусть G=(V, X) – граф, vОV, V1МV. Обозначим G(v)={wОV|{v, w}ОX} – образ вершины v; 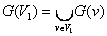 - образ множества вершин V1.
- образ множества вершин V1.