Динамические нагрузки, действующие на тяговый элемент цепных конвейеров

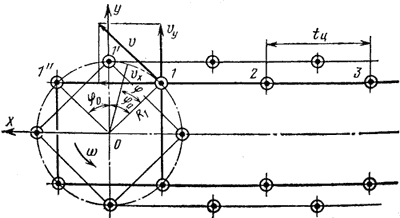
Основной отличительной чертой работы цепных конвейеров является то, что при огибании приводных звездочек или блоков тяговым элементом его скорость не остается постоянной. Это объясняется тем, что приводной элемент представляет собой многогранник и звено цепи при набегании на него располагается по хорде, а не по окружности, которую описывает зуб звездочки или точка пересечения граней блока (см. рис.).

Рис. Схема цепного привода конвейера.

Поэтому при постоянной угловой скорости звездочки (или блока) скорость цепи в направлении движения не остается постоянной.

Рассмотрим это подробнее, приняв для упрощения, что цепь абсолютно жесткая, а набегающая и сбегающая ветви цепи при любом положении звездочки или блока остаются параллельными сами себе.

При угловой скорости ω четырехгранного блока скорость шарнира цепи будет υ = ω*R₁ и направлена по касательной к окружности, описываемой точкой 1. Проекция этой скорости на ось X (на направление, совпадающее с направлением движения цепи) будет υ_x = ω*R₁*cos(ω*t - φ₀) где φ₀ — угол между вертикальной осью блока и радиусом R₁; он является началом отсчета текущего угла и взят со знаком минус, так как его откладывают от вертикальной оси блока в направлении, обратном вращению; ω*t = φ — текущее значение угла поворота, отсчитываемого от углаφ₀.

Проекция скорости шарнира цепи на ось У будет υ_Y= ω*R₁*sin(ω*t - φ₀)

При переходе шарнира в положение 1' угол φ изменяется от 0 до φ₀, а из положения 1' до положения 1" — от φ₀ до 2φ₀. По мере поворота блока и изменения угла φ величина скорости υ_x будет возрастать и в положении 1' скорость шарнира в направлении движения будет υ_x = ω*R₁, a υ_Y = 0. При дальнейшем повороте величина υ_x уменьшается и в положении 1" достигает снова минимальной величины υ_x = ω*R₁*cos(φ₀), a υ_Y будет увеличиваться до ω*R₁*sin(φ₀), имея обратное направление. Изменение скорости υ_Y незначительно влияет на натяжение цепи, поэтому в дальнейшем мы будем рассматривать только движение в направлении X.

Ускорение цепи по направлению ее движения будет
а_х = υ_x = -ω²*R₁*sin(ω*t - φ₀)

Рис. График скоростей и ускорений.

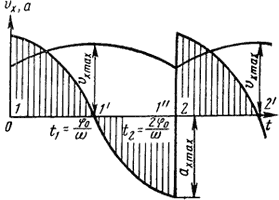
Для характерных точек получим (рис.):
положение 1
t = 0, υ_x = ω*R₁*cos(-φ₀), а_х = ω²*R₁*sin(φ₀);
положение 1'
t₁ = φ₀/ω, υ_x = ω*R₁, а_х = 0;
положение 1"
t₂ = 2*φ₀/ω, υ_x = ω*R₁*cos(-φ₀), а_х = -ω²*R₁*sin(φ₀);

Таким образом, при изменении угла φ от 0 до φ₀ цепь имеет положительное ускорение, а от φ₀ до 2φ₀ — отрицательное. Следовательно, движение цепи будет пульсирующим: ускоренным от положения 1 до 1' и замедленным от 1' до 1" с периодом колебаний t = 2φ₀/ω. Неравномерность движения цепи обусловливает возникновение в ней динамических усилий, тем больших по величине, чем больше ускорения и движущиеся массы.

Из графика (рис.) видно, что в момент времени захвата звездочкой следующего шарнира цепи ускорение изменяется от —а_Xmax до +а_Xmax т.е. на 2а_Xmax

Следовательно, динамическая сила, приложенная к цепи в тот момент, будет равна m2а_Xmax (m - масса цепи и гоуза) Учитывая, что эта сила прикладывается мгновенно вводят коэффициент динамичности (при изменении ускорения от —а_Xmax до +а_Xmax принимают К_д = 2), и тогда мгновенная динамическая сила (Н) будет
F_дXmax = K_дm2a_Xmax = 4ma_Xmax

К величине мгновенной динамической нагрузки необходимо прибавить величину силы инерции ma_Xmax, действующую на цепь в конце каждого периода изменения ускорения и имеющую отрицательный знак. Тогда суммарное значение динамической силы (Н) будет
F_д = F_дXmax - ma_Xmax = 3ma_Xmax
Поскольку R*sin(φ₀) = t_ц/2, а ω = πn/30 (t_ц — шаг цепи, n - частота вращения звездочки), то
a_Xmax = π²*n²*t_ц/30²*2 ≈ n²t_ц/180
и
F_д= 3m*n²*t_ц/180 = m*n²t_ц/60 (1)
Из выражения (1) видно, что динамическая нагрузка на цепь пропорциональна шагу цепи и квадрату частоты вращения блока (звездочки).

Динамические силы увеличивают общую нагрузку, действующую на тяговый элемент. Поэтому прочностной расчет (размеров цепи необходимо выполнять с учетом этих сил. Тогда полное расчетное усилие (Н) для цепи будет
Sp = S + Fд = S + m*n²*t_ц/60
или, имея в виду, что n = 60*υ/z*t_ц, где S — наибольшее усилие, определяемое при тяговом расчете, Н; m — приведенная масса элементов конвейера (цепи, груза) движущихся поступательно, кг.

Для конвейеров с простой трассой, имеющей только приводную и натяжную звездочки [силу тяжести рабочей и холостой ветвей можно определить как g(q + 2q_kL)], рекомендуется при определении величины m использовать следующую упрощенную зависимость:
m = k'q + kq_k где k'=1 для ковшовых, пластинчатых и т.п. конвейеров и h' 0,3...0,5 для скребковых, k - коэФФициент участия массы холостой ветви; при L<25м k=2; при L=26...60 м k= 1,5; при L>60 м k=1.

При больших скоростях тягового элемента проектируемого конвейера (υ > 0,75 м/с) для снижения инерционных нагрузок используют различные уравнительные приводы. Их назначение уменьшать или вовсе исключать неравномерность движения тягового элемента. Достигается это тем, что уравнительный привод сообщает приводной звездочке (блоку) неравномерную угловую скорость, изменяющуюся по закону, обратному изменению скорости υ_x тягового элемента, т. е. ωcos(ωt-φ₀)=υ_x/R₁=const

Рис. Уравнительный привод с короткозвенной цепной передачей: 1 — ведущая звездочка; 2 — цепь; 3 — зубчатый блок.

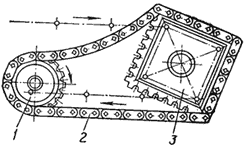
На рисунке показана схема уравнительного привода, состоящего из ведущей звездочки 1, цепи 2 с небольшим шагом и зубчатого блока 3, связанного с приводным блоком транспортера. Звездочке 1 сообщают постоянную угловую скорость, при этом блок 3 будет вращаться с переменной угловой скоростью, тем самым передавая тяговому элементу примерно постоянную скорость.

http://www.tehinf.ru/100200-chain-conveyor-cepnoj-konvejer.htm