Алгебраические операции
Алгебраическое произведение нечетких множеств A и B обозначается
Алгебраическая сумма этих множеств обозначается
Для операций ∙, 1) 2)
3)
4) В отличие от четких множеств, для нечетких множеств следующие свойства, вообще говоря, не выполняются: 1) 2) 3) При совместном использовании операций 1) 2) 3) 4) Умножение на число. Если α — положительное число такое, что
Дизъюнктивная сумма:
с функцией принадлежности
Выпуклая комбинация нечетких множеств. Пусть
Декартово (прямое) произведение нечетких множеств. Пусть
Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества. Пусть A — нечеткое множество, E — универсальное множество, и для всех элементов
где Пример 7. Пусть
Тогда
Четкое множество α-уровня (или уровня α;) Множеством α-уровня нечеткого подмножества A универсального множества E называется четкое подмножество
|

 к определяется так:
к определяется так: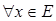

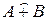 и определяется так:
и определяется так: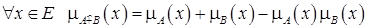
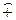 выполняются следующие свойства:
выполняются следующие свойства:
 (коммутативность);
(коммутативность);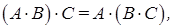
 (ассоциативность);
(ассоциативность);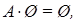
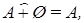
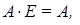
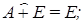
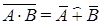 ,
,  (теоремы де Моргана).
(теоремы де Моргана).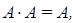
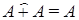 (идемпотентность);
(идемпотентность);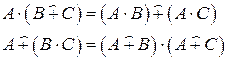 (дистрибутивность);
(дистрибутивность);
 .
. выполняются следующие свойства:
выполняются следующие свойства:
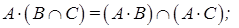


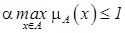 , то нечеткое множество
, то нечеткое множество 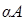 имеет функцию принадлежности
имеет функцию принадлежности 
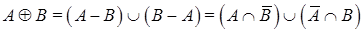
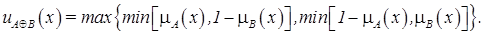
 нечеткие помножества универсального множества E, а
нечеткие помножества универсального множества E, а  неотрицательные числа, сумма которых равна 1. Тогда выпуклой комбинацией
неотрицательные числа, сумма которых равна 1. Тогда выпуклой комбинацией 

 — нечеткие подмножества универсальных множеств
— нечеткие подмножества универсальных множеств 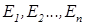 соответственно. Декартовым или прямым произведением
соответственно. Декартовым или прямым произведением  называется нечеткое подмножество множества
называется нечеткое подмножество множества  с функцией принадлежности
с функцией принадлежности
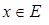 определены нечеткие множества
определены нечеткие множества  . Совокупность всех множеств
. Совокупность всех множеств 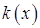 называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на нечеткое множество A является нечеткое множество вида
называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на нечеткое множество A является нечеткое множество вида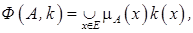
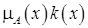 — произведение числа на нечеткое множество.
— произведение числа на нечеткое множество.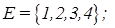
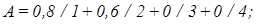




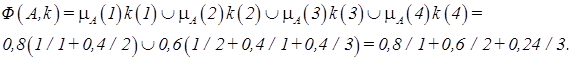
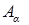 универсального множества E, определяемое в виде
универсального множества E, определяемое в виде 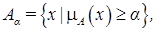 где
где