Порядок проведения лабораторной работы
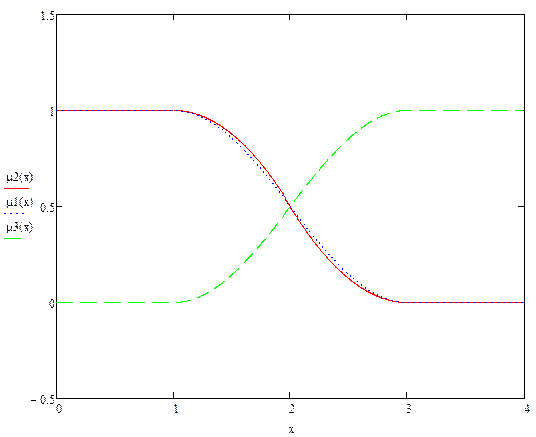
5.1 Представление функции принадлежности в 2х видах (μ1 и μ 2) (из S-образной группы функций) и нахождение обратной к ней функции (μ 3).
5.2. Применение логических операций на начеткие множества μ1 и обратной к ней μ3
Пересечение (μ4):
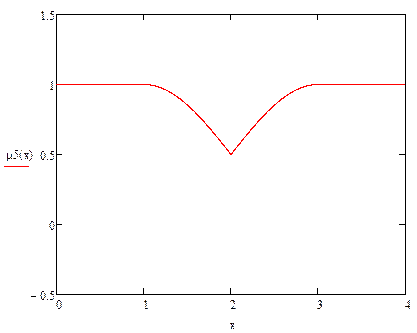
Объединение (μ5):
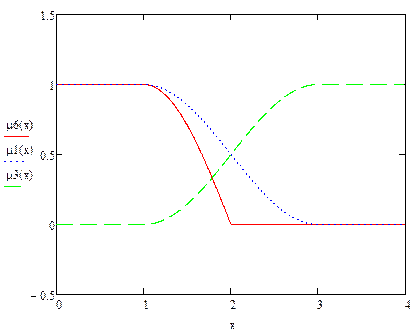
Логическая разность (μ6):
5.3. Приминение алгебраических операций на начеткие множества μ1 и обратной к ней μ3
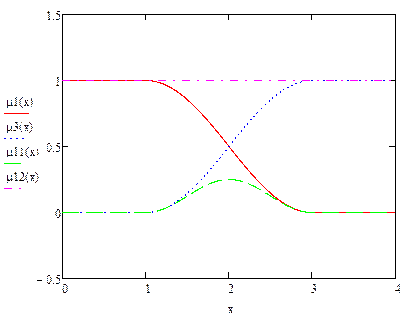
Алгебраическая сумма (μ12) и алгебраическое произведение (μ11)
:
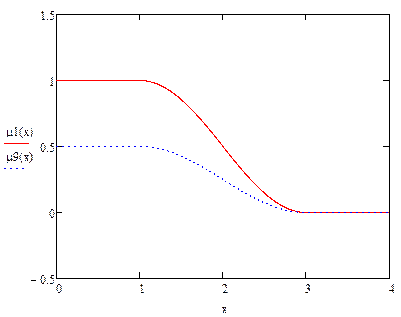
Умножение на число (μ9):
Дизъюнктивная разность (μ8):
Выпуклая комбинация нечетких множеств (μ10):
Выводы В качестве выводов необходимо: перечислить рассмотренные на лабораторном занятии вопросы; перечислить рассмотренные на лабораторном занятии функции принадлежности (например: S-образные, Z-образные и П-образные функции принадлежности); особенности трансформации функций принадлежности при изменении их параметров; особенности реализации логических и алгебраических операций в приложение MathCad для используемых функций.
6. Контрольные вопросы 1. Приведите пример нечеткого множества. 2. Дайте определение четкого множества, используя характеристическую функцию принаддежности. 3. Дайте определение нечеткого множества, используя характеристическую функцию принадлежности. 4. Что такое функция принадлежности? (Ее описание, определение, назначение.) 5. Перечислите основные характеристики нечетких множеств. 6. Зачем нужны нечеткие множества и нечеткая логика? 7 Когда и кто разработал теорию нечетких множеств и нечеткой логики? 8. Как можно задавать нечеткие множества и строить функции принадлежности? 9. Дайте определение алгебраического произведения 10. Укажите, какие свойства выполняются для операций 11. Дайте определение декартова произведения нечетких множеств. 12. Что называется четким множеством α-уровня?
Список литературы
1. Лекции по СИИ (Веселов Ю.Г.) 2. Меньшаков Ю.К. Теоретические основы технических разведок: Учеб. Пособие/Под ред Ю.Н. Лаврухина. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. С. 3-5. 3. Леоненков А.В. Нечеткое моделирование в среде MATLAB fuzzyTECH. СПб.: БХВ-Петербург, 2003. С. 11-171. 4. Чулюков В.А., Астахова И.Ф. и др. Системы искусственного интеллекта. Практический курс: Учебное пособие/под ред. И.Ф. Астаховой. М.: БИНОМ. Лаборатория знаний, 2008. С. 80-97.
|

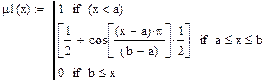
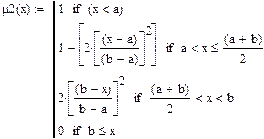

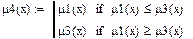

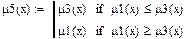
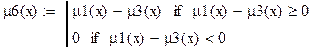
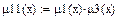
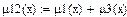
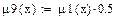
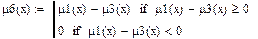
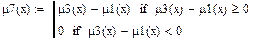
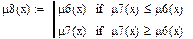
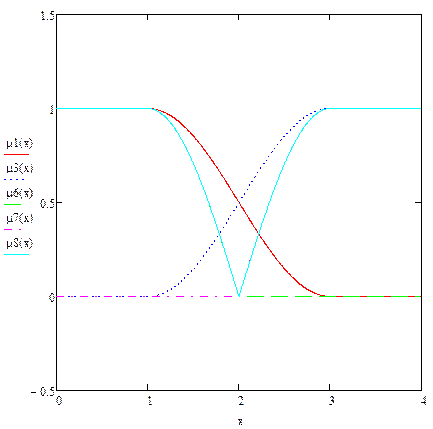
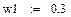
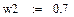
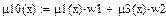

 алгебраической суммы
алгебраической суммы 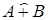 , дизъюнктивной суммы
, дизъюнктивной суммы 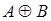 множеств A и B
множеств A и B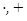 .
.


