Примеры. 1. Рассмотрим множество Uвсех действительных чисел от 0 до 10, которое назовем универсальным
1. Рассмотрим множество Uвсех действительных чисел от 0 до 10, которое назовем универсальным. Определим подмножество Aмножества Uвсех действительных чисел от 5 до 8:
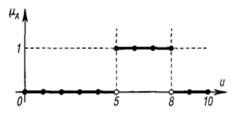
Рис. 1 - Характеристическая функция множества А
Рассмотрим характеристическую функцию множества A, эта функция ставит в соответствие число 1 или 0 каждому элементу из II в зависимости от того, принадлежит данный элемент подмножеству A или нет. Ее график представлен на рис. 1. Элементы, которым поставлено в соответствие число 1, можно интерпретировать как элементы, принадлежащие множеству A, а элементы, которым поставлено в соответствие число 0, как элементы, не принаде-жащие множеству A. Эта концепция используется во многих областях приложений. Но можно легко обнаружить ситуации, в которых данной концепции будет недоставать гибкости. 2. В данном примере опишем множество молодых людей, которое формально можно записать так:
Так как вообще возраст начинается с 0, то нижний предел этого множества должен быть нулем. Верхний предел определить немного сложнее. На первый раз установим верхний предел, скажем, равным 20 годам. Таким образом, получаем B как четко ограниченный интервал, буквально:
Возникает вопрос: почему кто-то в свой двадцатилетний юбилей — молодой, а сразу на следующий день уже не молодой? Очевидно, это структурная проблема, и если передвинуть верхнюю границу в произвольную точку, то можно задаться точно таким же вопросом. Более естественный путь получения множества В состоит в ослаблении строгого разделения на молодых и не молодых. Сделаем это, вынося не только (четкие) суждения «Да, он/она принадлежит множеству молодых людей» или «Нет, он/она не принадлежит множеству молодых людей», но и более гибкие формулировки: «Да, он/она принадлежит к достаточно молодым людям» или «Нет, он/она не очень молод/молода». Далее рассмотрим, как с помощью нечеткого множества определить такое выражение, как «он/она еще молод/молода». В первом примере мы кодировали все элементы универсума рассуждения с помощью чисел 0 или 1. Простой способ обобщить данную концепцию — ввести значения между 0 и 1. Реально можно даже допустить бесконечное число значений между 0 и 1, называемое единичным интервалом
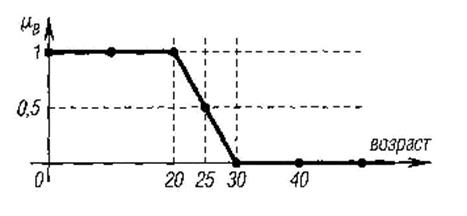
Рис. 2. Характеристическая функция множества молодых людей
Интерпретация чисел при соотнесении всех элементов универсума рассуждений становится теперь более сложной. Конечно, снова число 1 ставится в соответствие (соотносится) тому элементу, который принадлежит множеству B, а 0 означает, что элемент точно не принадлежит множеству B. Все другие значения определяют степень принадлежности ко множеству B. Для наглядности приведем характеристическую функцию множества молодых людей, как и в первом примере (рис. 2). Согласно ее графику, 25-летние все еще молоды со степенью уверенности 50 процентов.
Более строгое представление о нечетких множествах Пусть E — универсальное (universal) или несущее множество, x — элемент E, а K — некоторое свойство. Определим для несущего множества E обычное (четкое) подмножество A, элементы которого удовлетворяют свойству R, как множество упорядоченных пар
где Нечеткое подмножество отличается от обычного тем, что для элементов x из множества E нет однозначного ответа «да—нет» относительно свойства K. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченных пар с характеристической функцией принадлежности. Функция принадлежности указывает степень (или уровень) принадлежности элемента x подмножеству A. Множество M называется множеством принадлежности. Если Пример 3. Пусть имеется обычное множество
и пусть задано A — нечеткое множество, для которого
Тогда нечеткое множество A можно представить в виде
или
где знак «+» не является обозначением операции сложения, а имеет смысл объединения.
Основные характеристики нечетких множеств Пусть Тогда высотой нечеткого множества называется верхняя граница значений его функции принадлежности: Нормальным называется нечеткое множество, высота которого равна 1. Если высота меньше 1, нечеткое множество называется субнормальным. Говорят, что нечеткое множество пусто, если Непустое субнормальное множество можно нормализовать по формуле
Нечеткое множество является унимодальным, если Носителем нечеткого множества A(обозначается как supp A)является обычное подмножество со свойством Элементы Примеры нечетких множеств и их характеристик
Рассмотрим примеры нечетких множеств.
|


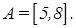
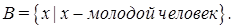
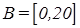 .
.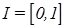
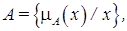
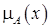 — характеристическая функция, принимающая значение 1, если элемент x удовлетворяет свойству R, и 0 — в противном случае.
— характеристическая функция, принимающая значение 1, если элемент x удовлетворяет свойству R, и 0 — в противном случае.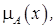 принимающей значения в некотором вполне упорядоченном множестве M, например,
принимающей значения в некотором вполне упорядоченном множестве M, например, 
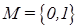 , то нечеткое подмножество A может рассматриваться как обычное или четкое множество.
, то нечеткое подмножество A может рассматриваться как обычное или четкое множество.
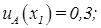
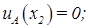
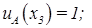
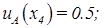
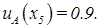

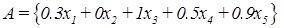
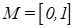 и A — нечеткое множество с элементами из универсального (несущего) множества E и множеством принадлежности M.
и A — нечеткое множество с элементами из универсального (несущего) множества E и множеством принадлежности M.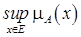
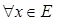
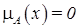 .
.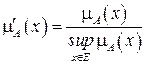 .
.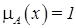 только на одном элементе x из универсального множества E.
только на одном элементе x из универсального множества E. , т. е. supp
, т. е. supp 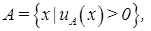
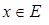 , для которых
, для которых 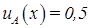 , называются точками перехода множества A.
, называются точками перехода множества A.


