Логические операции
Включение. Пусть A и B — нечеткие множества на универсальном множестве E. Говорят, что A содержится в B, если
Обозначение: Например, если A — множество чисел, очень близких к 10, а B — множество чисел, близких к 10, то Иногда используют термин доминирование, т. е. в случае, когда Множества A и Bравны, если Объединение. Объединением нечетких множеств A и B называется нечеткое множество, обозначаемое
Иначе говоря, объединением
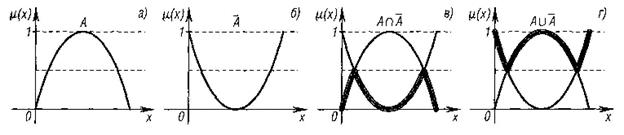
Рис. 5. - Операции с нечеткими множествами: а) подмножество и дополнение нечеткого множества; б) разность нечетких множеств; в) объединение нечетких множеств; г) пересечение нечетких множеств
Пересечение. Пересечением
Дополнение. Дополнение Это определение можно сформулировать иначе. Пусть
Разность. Разностью
На рис. 5 проиллюстрированы данные выше определения. Операции над нечеткими множествами можно проиллюстрировать и так, как показано на рис. 6. Введенные операции над нечеткими множествами основаны на использовании операций max и min. В теории нечетких множеств разрабатываются вопросы построения обобщенных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им связок И, ИЛИ, НЕ.
Рис. 6. Графическая интерпретация логических операций: а) нечеткое множество А; б) нечеткое множество А; в) А л А; г) А у А
Для операций пересечения и объединения выполняются следующие свойства (A, B, C - нечеткие множества; - Ø – пустое множество, т.е. 1) 2)
3) 4)
5) 6) 7) 8) 9) В отличие от четких множеств, для нечетких множеств в общем случае имеем:
|

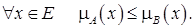 (1)
(1)
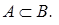
 и
и 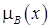 — характеристические функции, то из неравенства (1) следует, что если некоторый элемент x принадлежит множеству A, т. е.
— характеристические функции, то из неравенства (1) следует, что если некоторый элемент x принадлежит множеству A, т. е. 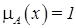 , то он принадлежит и множеству B, поскольку
, то он принадлежит и множеству B, поскольку  .
.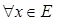
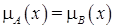 . Обозначение: A = B.
. Обозначение: A = B.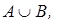 функция принадлежности которого определяется следующим образом:
функция принадлежности которого определяется следующим образом: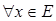

 называется наименьшее нечеткое подмножество, включающее как A, так и B.
называется наименьшее нечеткое подмножество, включающее как A, так и B.
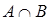 называется наибольшее нечеткое подмножество, содержащееся одновременно в множествах A и B:
называется наибольшее нечеткое подмножество, содержащееся одновременно в множествах A и B: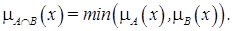 (2)
(2)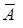 нечеткого множества A имеет функцию принадлежности
нечеткого множества A имеет функцию принадлежности 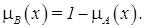 Обозначение:
Обозначение: 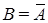 или
или 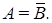
 A и B — нечеткие множества, заданные на E. Множество A и B дополняют друг друга, если
A и B — нечеткие множества, заданные на E. Множество A и B дополняют друг друга, если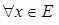
 Очевидно, что
Очевидно, что 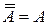 .
. называют множество с функцией принадлежности
называют множество с функцией принадлежности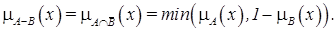
 E - универсальное множество):
E - универсальное множество):
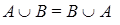 (коммутативность);
(коммутативность);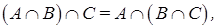
 (ассоциативность);
(ассоциативность);
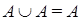 (идемпотентность);
(идемпотентность);
 (дистрибутивность)
(дистрибутивность)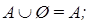


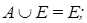
 (теоремы де Моргана).
(теоремы де Моргана).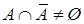 ,
,