Примеры. 4.Пусть Нечеткое множество «несколько» можно определить следующим образом:
4. Пусть
Его 5. Пусть
Нечеткое множество «молодой» на универсальном множестве
где х — возраст Сидорова. Для каждого
6. Пусть Е = {Запорожец, Жигули, Мерседес,...} — множество марок автомобилей, а 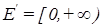 — универсальное множество «стоимость», тогда на — универсальное множество «стоимость», тогда на 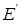 мы можем определить нечеткие множества с помощью функций принадлежности, графики которых изображены на рис. 5.3. Имея эти функции и зная стоимости автомобилей из E в данный момент времени, мы тем самым мы можем определить нечеткие множества с помощью функций принадлежности, графики которых изображены на рис. 5.3. Имея эти функции и зная стоимости автомобилей из E в данный момент времени, мы тем самым
Рис. 3. - Графики функций принадлежности нечетких множеств из примера 6.
определим на
Так, нечеткое множество «для бедных», заданное на универсальном множестве Е, показано на рис. 5.4. Рис. 4. - График функции принадлежности нечеткого множества «для бедных» Аналогично можно определить нечеткие множества «скоростные», «средние», «тихоходные» и т. д. В рассмотренных выше примерах использованы прямые методы, когда эксперт либо просто задает для каждого При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкретное лицо и каждый должен дать один из двух ответов: «этот человек лысый» или «этот человек не лысый». Тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение
|


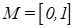 Нечеткое множество «несколько» можно определить следующим образом:
Нечеткое множество «несколько» можно определить следующим образом:
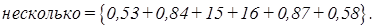

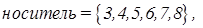 точки перехода -
точки перехода - 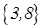 .
.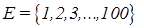 и это множество соответствует понятию «возраст». Тогда нечеткое множество «молодой» может быть определено с помощью функции принадлежности
и это множество соответствует понятию «возраст». Тогда нечеткое множество «молодой» может быть определено с помощью функции принадлежности
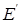 = {Иванов, Петров, Сидоров, …} задается с помощью функции принадлежности
= {Иванов, Петров, Сидоров, …} задается с помощью функции принадлежности 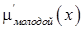 на
на  (возраст), называемой по отношению к E функцией совместимости. При этом
(возраст), называемой по отношению к E функцией совместимости. При этом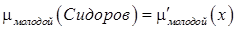 ,
,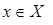 величина
величина 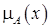 интерпретируется как степень принадлежности элемента х нечеткому множеству А. В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение
интерпретируется как степень принадлежности элемента х нечеткому множеству А. В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение  — степенью принадлежности элемента x нечеткому множеству A.
— степенью принадлежности элемента x нечеткому множеству A.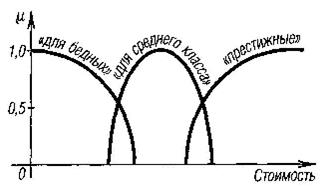
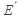 нечеткие множества «для бедных», «для среднего класса», «престижные».
нечеткие множества «для бедных», «для среднего класса», «престижные».
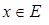 значение
значение 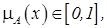 формируя векторную функцию принадлежности
формируя векторную функцию принадлежности 
 для данного лица.
для данного лица.


