Вероятностный способ расчета размерных цепей
При выводе формул для расчета размерных цепей способом на максимум-минимум предполагали, что в процессе обработки или сборки возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих размеров или обратное их сочетание. Любое из этих сочетаний обеспечивает наименьшую точность замыкающего звена, но они мало вероятны, так как отклонения размеров в основном группируются около середины поля допуска и соединения деталей с такими отклонениями встречаются наиболее часто. Особенно это характерно для серийного и массового производства при оптимально настроенном оборудовании, как было отмечено ранее, если допустить ничтожно малую вероятность (например, 0,27 %) несоблюдения предельных значений замыкающего размера, можно значительно расширить допуски составляющих размеров и тем самым снизить себестоимость изготовления деталей. На этих положениях и основан вероятностный способ расчета размерных цепей. Полагая, что погрешности изготовления составляющих и замыкающего размеров подчиняются закону нормального распределения, а границы их вероятного рассеивания (при зоне v=6 σ;) совпадают с границами полей допусков, можно принять ТА∆= 6σA∆ или σA∆ = ТА∆ /6, σ- это единица рассеивания. При этом у 0,27 % изделий размеры замыкающих звеньев могут выходить за пределы поля допуска. Выполнив некоторые расчеты и преобразования с учетом положений теории вероятности [4] можно получить уравнение для определения допуска замыкающего звена
(Х) совпадает со серединой поля допуска, а зона рассеивания (v) со значением допуска. В производственных условиях в результате совместного влияния систематических и случайных погрешностей центр группирования может не совпадать с серединой поля допуска, зона рассеивания не равна величине допуска, а распределение подчиняется не обязательно закону Гаусса. Для определения допуска замыкающего звена при произвольном или неизвестном законе распределения вводят дополнительные коэффициенты: t – коэффициент риска, который выбирается из таблицы 3 в зависимости от заданного процента риска P [ 1 ], Таблица 3 Значение коэффициента риска
λi, кi - коэффициенты относительного рассеивания, характеризующие закон распределения размеров При нормальном законе распределения размеров составляющих звеньев (закон Гаусса) λi2 =1/9; кi=1; При распределении по закону треугольника (закон Симпсона) λi2 =1/6; кi=1,22; При распределении по закону прямоугольника (закон равной вероятности) λi2 =1/3; кi=1,73; значения коэффициента кi определены опытным путем профессором Н.А.Бородачёвым и приведены в справочной литературе (издание Академии наук СССР, 1943 г.). Вообще, существует два вида обозначения и значений коэффициентов относительного рассеивания λi и кi . О ни введены для перехода от средних квадратических отклонений σ;к полям допусков и зонам рассеивания размеров при разных законах распределения и связаны между собой зависимостью [2]:
В настоящее время в нормативных материалах [1] и справочниках [2,3] дается коэффициент λi. В случае необходимости применения коэффициента кi следует обращаться к литературе [4,7] или взять значения из данного пособия. В общем виде формула для определения допуска замыкающего звена учитывает еще коэффициент ξi,но поскольку решение пространственных размерных цепей сводится к решению плоских линейных цепей с параллельными звеньями, то коэффициент ξi берется равным 1(ξi=1). Итак, допуск замыкающего звена при вероятностном способе расчета определяется по формулам (18), (19).
При законе Гаусса мы принимаем t=3, ξi =1, кi=1, λi= 1/3, λi2=1/9, т.е. формулы упрощаются, и допуск замыкающего звена определяется по формуле (17)
Для других законов распределения при выборе значений следует пользоваться таблицей 4. Таблица 4 Значения коэффициентов для расчета ТА'∆
После расчета значения допуска замыкающего звена определяют наибольшее и наименьшее значения замыкающего звена из выражений (20) и (21), при этом отклонения и номинальные значения звена берут из расчета на max-min.
Итак, нами рассмотрены два способа определения замыкающего звена, применяемые при решении размерных цепей методом полной и неполной взаимозаменяемости. При применении других методов расчета, в частности, метода групповой взаимозаменяемости (селективной сборки), первоначальный расчет цепи также ведется способом на max-min.
|

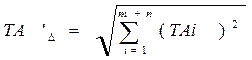 (17).
(17). Но формула (17) выведена из предположения, что распределение размеров всех составляющих звеньев подчиняется закону Гаусса, центр рассеивания
Но формула (17) выведена из предположения, что распределение размеров всех составляющих звеньев подчиняется закону Гаусса, центр рассеивания
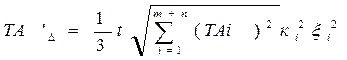 (18)
(18)
 (19)
(19)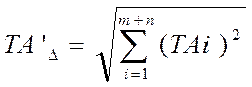

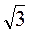 =1,73
=1,73
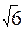 /2=1,225
/2=1,225
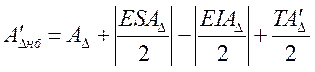 (20)
(20)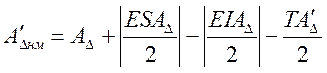 (21)
(21)


