Пример расчета размерной цепи
Расчет размерной цепи является одним из заданий курсовой работы по дисциплине «Метрология, стандартизация, сертификация». Поэтому наряду с изложением теоретических вопросов по размерным цепям нами дан пример расчета размерной цепи. Рассматривается обратная задача – определение замыкающего звена по известным составляющим звеньям. Задача решена двумя методами и двумя способами. Методические рекомендации по решению данной задачи даны в методических указаниях [8,9]. В данном пособии она приводится для закрепления изложенного материала и возможности воспользоваться данным примером без дополнительных справочников и учебных пособий при выполнении курсовой работы. Студенту выдается эскиз детали или узла с указанием замыкающего или исходного звена (обозначение с символом ∆). Поставлен тип задачи: первая -прямая (технологическая), вторая –обратная (конструкторская). Размерными линиями указаны размеры, заданные в качестве звеньев для составления цепи. Другие размеры для составления цепи не назначать. Номинальные размеры звеньев определяются по чертежу в зависимости от масштаба, указанного в задании. Квалитет звеньев также указан в задании. Требуется: 1. Составить размерную цепь. 2. Рассчитать размерную цепь двумя методами: - методом полной взаимозаменяемости (способ расчета на max-min); - методом неполной взаимозаменяемости (вероятностный способ расчета на основании расчета на max-min); 3. Сделать графическую проверку способов расчета. Последовательность расчетов при решении первой и второй задач для обоих методов и примеры расчета приводятся в литературе [1,2,3,9]. Все термины, определения и обозначения, применяемые в расчетах, должны соответствовать РД 50-635-87 [1]. при назначении допусков на составляющие звенья следует руководствоваться правилом: допуск задается «в тело детали», т.е. для наружных диаметров, высоты, длины, ширины, толщины детали «в минус», по посадкам с полями отклонений h. Для внутренних диаметров, размеров на глубину, внутренних габаритов в корпусных деталях – «в плюс», т.е. – поля Н с соответствующим квалитетом точности. При составлении схемы размерной цепи, если не указана база, деталь (узел) следует обходить по заданному контуру, придерживаясь понятий увеличивающих и уменьшающих звеньев по часовой стрелке.
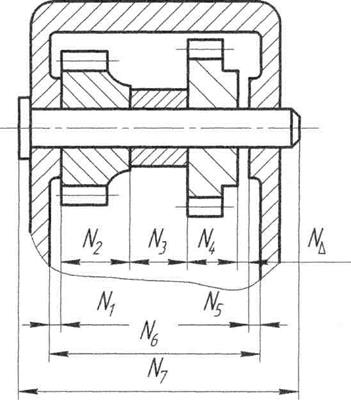
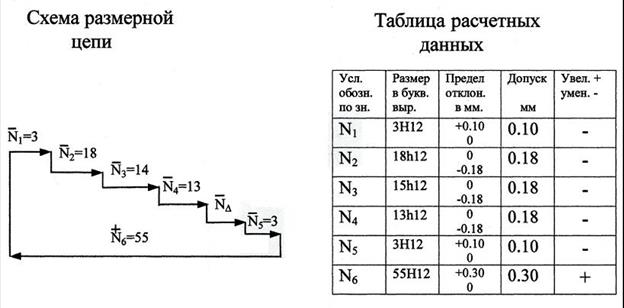
ПРИМЕР:Рассчитать размерную цепь для узла. Выдан эскиз (рис.11). В задании указан масштаб размеров (М 1:1) и квалитеты точности составляющих звеньев – 12 квалитет. Требуется определить величину замыкающего звена N∆ по известным составляющим звеньям. Тип задачи – обратная. Рис.11 Решение 1. Составляем схему размерной цепи и таблицу расчетных данных (рис. 12): Все размеры составляющих звеньев берем с чертежа в масштабе, указанном в задании, допуск назначаем “в тело” детали, т.е. для наружных размеров в «(-)», для внутренних размеров в «(+)».
Рис.12 2. Составляем уравнение номинальных размеров и определяем N1 + N2 + N3 + N4+ N D = N6 - N1 - N2 - N3 - N4 - N5 = 55 - 3 - 18 - 15 - 13 - 3 = 3 мм 3. I метод - метод полной взаимозаменяемости (способ на max - min). 3.1 Определяем допуск замыкающего звена.
3.2 Находим координату середины поля допуска замыкающего звена. Координата определяется с учетом знака отклонения.
3.3 Определяем верхнее и нижнее предельные отклонения замыкающего размера:
или отклонения звена В.О. =300 - (- 180 - 180 - 180) = 840 мкм Н.О. = 0 - 100 - 0 - 0 - 100 = - 200 мкм
3.4 Записываем предельные значения N∆
4.II Метод неполной взаимозаменяемости (вероятностный способ расчета). 4.1 Рассчитываем
при этом принимаем t = 3,
4.2 Определяем
Значения ESN∆, EJN∆ рассчитаны в п.3.3
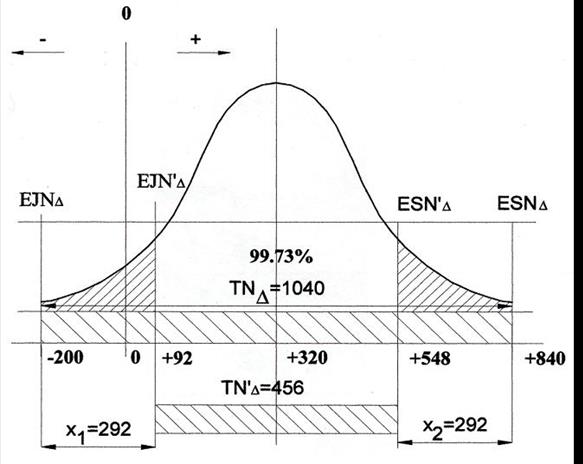
При этом: 4.3 Производим графическую проверку (рис.13). проверочное условие: Х1=Х2
ВЫВОД: При расчете методом неполной взаимозаменяемости предусмотрен выход размеров замыкающего звена за пределы поля допуска рассматриваемого
Графическая проверка
Рис.13
|


 .
.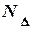 + N5= N6
+ N5= N6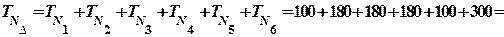 1040 мкм
1040 мкм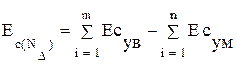
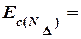 150 - (+ 50 - 90 - 90 - 90 + 50) = 150 - (- 170) = 320 мкм
150 - (+ 50 - 90 - 90 - 90 + 50) = 150 - (- 170) = 320 мкм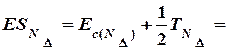 320 + 1040/2 = 840 мкм
320 + 1040/2 = 840 мкм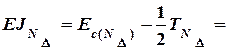 320 - 1040/2 = - 200 мкм
320 - 1040/2 = - 200 мкм можно определить через отклонения
можно определить через отклонения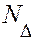 или
или 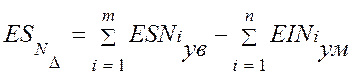 =
= или
или 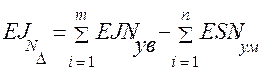 =
=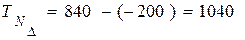 мкм
мкм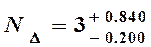
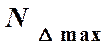 = 3,840 мм
= 3,840 мм 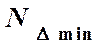 = 2,800 мм
= 2,800 мм по формуле:
по формуле: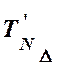 =
= 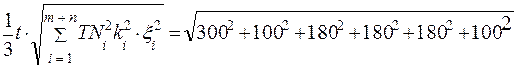 = =57,384 мкм
= =57,384 мкм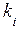 = 1,
= 1, 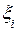 = 1, т.е. принимаем условия: процент риска Р равен 0,27 (табл.3), распределение размеров всех звеньев цепи по закону Гаусса, цепь плоская, линейная.
= 1, т.е. принимаем условия: процент риска Р равен 0,27 (табл.3), распределение размеров всех звеньев цепи по закону Гаусса, цепь плоская, линейная.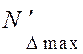 и
и  по формулам
по формулам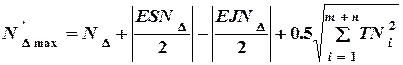
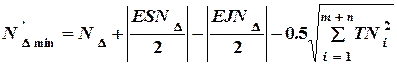
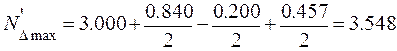 мм
мм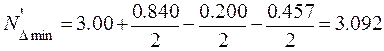 мм,
мм,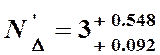 .
.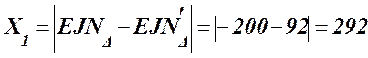 мкм
мкм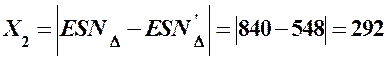 мкм
мкм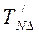 , т.е. определенное количество неучтенных звеньев – брак, величина которого составляет 0,27 %.
, т.е. определенное количество неучтенных звеньев – брак, величина которого составляет 0,27 %.