Пример расчёта трёхфазной цепи
3.2.1. Нагрузка симметричная
Рис. 10
Определить фазные и линейные токи, активную мощность каждой фазы и всей трёхфазной нагрузки. Построить векторную диаграмму напряжений.
РЕШЕНИЕ
Учитывая, что нагрузка симметричная, находим фазные токи:
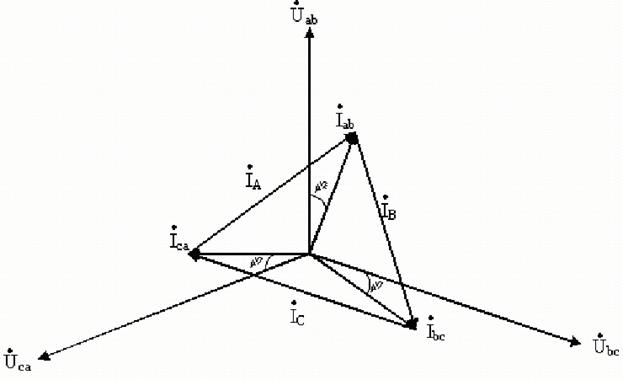
. а) строим базис – тройку симметричных векторов фазных (они же линейные) напряжений б) строим вектора фазных токов в) на основании уравнений состояния в соответствии с первым законом Кирхгофа строим вектора линейных токов
Рис.11
Задача 4. Данные и требования такие же, как и в задаче 3. Отличие в типе соединения: вместо треугольника соединение звезда. (рис.12)
Рис.12
Решение 1. При соединении “звезда”
2. Фазные (они же линейные) токи определим на основании закона Ома
3. Фазная активная мощность 4. Активная мощность всей трёхфазной нагрузки 5.
Рис. 13 а) строим базисную тройку векторов фазных напряжений б) в сторону опережения по фазе (нагрузка активно-ёмкостная) под углом
Угол
в) на основании второго закона Кирхгофа вектора линейных напряжений
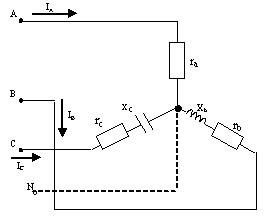
Задача 5. В трехфазную четырехпроводную линию с симметричным линейным напряжением U включен электроприемник, собранный по схеме «звезда» (см. рис. 14). Даны сопротивления фаз
Рис. 14
Определить фазные и линейные токи, ток в нейтральном проводе, активную мощность всей цепи и каждой фазы в отдельности.
РЕШЕНИЕ
a) строим базисную тройку симметричных векторов фазных напряжений под соответствующими углами сдвигов фаз строим вектора фазных (они же линейные) токов, задавшись при этом определенным масштабом.
- вектор тока
- вектор
- вектор
б) строим вектор тока нейтрального провода циркуля) вектора
Замеряем линейкой длину вектора тока
Замечание: Длину вектора
|

 Задача 3. В трёхфазную трёхпроводную цепь с симметричным линейным напряжением
Задача 3. В трёхфазную трёхпроводную цепь с симметричным линейным напряжением 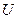 включён трёхфазный электроприёмник, собранный по схеме треугольник (рис.10)
включён трёхфазный электроприёмник, собранный по схеме треугольник (рис.10)


 .
.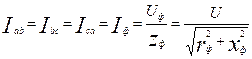
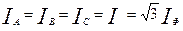


 ,
, 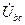 ,
, 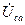 . (См рис.11);
. (См рис.11); и
и 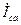 под углом сдвига фаз
под углом сдвига фаз 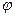 к соответствующим векторам фазных напряжений в сторону отставания
к соответствующим векторам фазных напряжений в сторону отставания 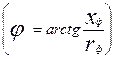 ;
;
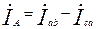

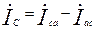


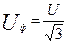

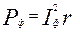
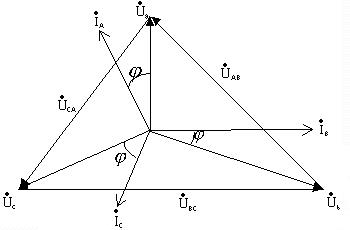
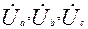 ;
;
 ;
;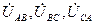 найдем исходя из следующих уравнений:
найдем исходя из следующих уравнений: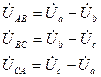

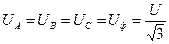

 ,
, 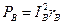 ,
, 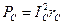
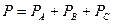
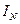 в нейтральном проводе найдем графическим методом с помощью векторной диаграммы (Рис.15.):
в нейтральном проводе найдем графическим методом с помощью векторной диаграммы (Рис.15.):
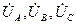 ,
, совпадает по фазе с вектором
совпадает по фазе с вектором 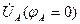 т.к. сопротивление фазы А чисто активное. Длина вектора определяется выбранным масштабом.
т.к. сопротивление фазы А чисто активное. Длина вектора определяется выбранным масштабом. отстает по фазе от вектора
отстает по фазе от вектора 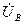 на угол
на угол  т.к. фаза В имеет активно-индуктивный характер сопротивления. Длина вектора
т.к. фаза В имеет активно-индуктивный характер сопротивления. Длина вектора  откладывается по транспортиру.
откладывается по транспортиру. опережает
опережает 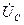 на угол
на угол 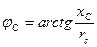
 , для этого складываем (с помощью
, для этого складываем (с помощью
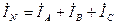 (на основании первого закона Кирхгофа)
(на основании первого закона Кирхгофа) .
.


