Пример расчёта сложных эл. цепей.(содержащих несколько источников питания).

В этом случае можно пользоваться методом непосредственного применения законов Кирхгофа или методом контурных токов.

 

Алгоритм метода непосредственного применения законов Кирхгофа:

1. Если цепь содержит последовательные и параллельные соединения, её упрощают, заменяя эти соединения эквивалентными;
2. обозначают токи во всех ветвях (I₁, I_{2 …} I _m ), произвольно выбирают их положительные направления и обозначают на схеме эти направления стрелкам;
3. составляют по первому закону Кирхгофа уравнения для (n-1) узлов.(n-число узлов в схеме)
4. недостающие m-(n-1) уравнения получают по второму закону Кирхгофа, для чего выбирают в схеме m-(n-1), взаимно независимых контуров (m-число ветвей).

В результате получается система из m уравнений. Решение этой системы позволяет определить не только числовые значения токов, но и их действительные направления. Если решение привело к отрицательному знаку для какого-либо тока, то его действительное направление противоположно произвольно выбранному в пункте 2.

 

Пример В качестве иллюстрации рассмотрим цепь, схема которой изображена на рис.4. Схема содержит 6 ветвей и 4 узла (m = 6, n = 4). На схеме обозначены выбранные положительные направления всех шести токов.

В соответствии с пунктом 3 по первому закону Кирхгофа составляем 3 уравнения (4-1=3) для узлов a,b,c.

узел а: I₁ – I₂ - I₃=0;

узел b: I₂+I₄+ I₅=0;

узел с: -I₄ - I₅ - I₆=0.

В соответствии с пунктом 4 по второму закону Кирхгофа составляем 3 уравнения (6-3=3) для контуров adеa, abcda, bfcb (направления обхода принимаем по часовой стрелке):

контур adea: E₁= I₁ (r₀₁+r₁) + I₃r₃

контур abcda: 0 = I₂r₂-I₄r₄+I₆r₇-I₃r₃

контур bfcb: -E₂ = -I₅ (r₅+r₀₂+r₆) + I₄r₄

Таким образом, при расчёте данной цепи по методу непосредственного применения законов Кирхгофа приходиться решать систему из шести уравнений.

 

	r1		r2		r5
		a			b

E1

r01

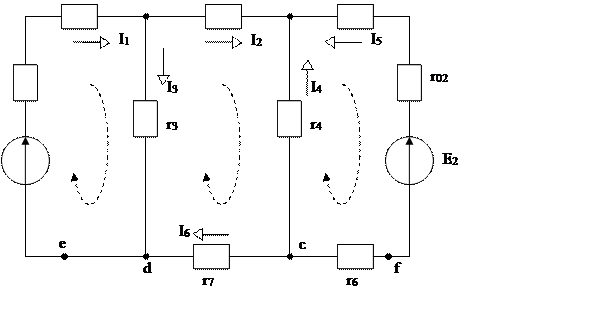
Рис.4

 

Метод контурных токов позволяет уменьшить количество уравнений вдвое!

 

Алгоритм метода контурных токов:

1. Выбирают в схеме взаимно независимые контуры (так, чтобы одна из ветвей соответствующего контура входила только в этот контур).
2. для выбранных независимых контуров принимают произвольно направления контурных токов в них;
3. составляют для выбранных контуров уравнения по второму закону Кирхгофа относительно контурных токов.

Для цепи, изображённой на рис.4, выбирая прежние независимые контуры и принимая указанные на рис. 5 направления контурных токов I_I, I_II, I_III получим следующие три уравнения:

E₁ = I_I (r ₀₁+r₁+r₃) - I_II r₃;

0 = – I_I r₃+ I_II (r₂+r₄+r₇+r₃) – I_III r₄

-E₂ = – I_II r_{4 +} I_III (r₀₂+r₆+r₄+r₅)_.

	r1		r2		r5

r01

E1

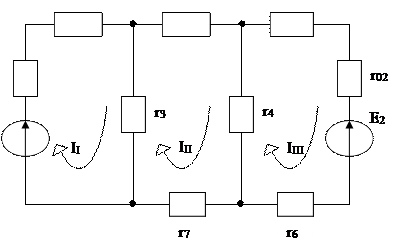
Рис.5.

 

 

После того как найдены контурные токи, определяют действительные токи в ветвях. В ветвях, не являющихся общими для смежных контуров, найденный контурный ток будет равен действительному току ветви. В ветвях, общих для смежных контуров, действительный ток равен алгебраической сумме контурных токов. Таким образом, в рассматриваемом примере действительные токи равны (см. рис.4 и рис.5):

I₁ = I_I; I₂ = I_II; I₃ = I_I -I_II; I₄ = I_III-I_II; I₅= -I_III ; I₆ = I_II; (I₂=I₆)