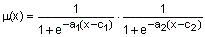Демонстрационные примеры 3 страница

1. data – матрица данных “входы – выход”. Каждая строка данных содержит одну пару “входы – выход”. Последний столбец матрицы содержит значения выходной переменной, а остальные – значения входных переменных;
2. mf_n – вектор, задающий количество термов, которыми оценивается каждая входная переменная. Если аргумент задан скалярным значением, то количество термов принимается одинаковым для всех входных переменных. Значение по умолчанию – 2;
3. mf_type – матрица стрингов, определяющая тип функций принадлежности для каждой входной переменной. Если аргумент задан одним стрингом, тогда все функции принадлежности будут иметь один и тот же тип. Значение по умолчанию - 'gbellmf' (обобщенная колокообразная функция принадлежности). Функция genparam не поддерживает следующие типы функции принадлежностей: 'sigmf', 'smf' и 'zmf'.

Функция genparam возвращает матрицу mf_param, каждая строчка которой содержит параметры одной функций принадлежности. Первая строка матрицы соответствует параметрам первой функции принадлежности первой входной переменной, вторая - второй функции принадлежности первой входной переменной, …, последняя - последней функции принадлежности последней входной переменной.

Пример:

NumData = 1000;
data = [rand(NumData,1) 10*rand(NumData,1)-5 rand(NumData,1)];
NumMf = [3 7];
MfType = str2mat('trapmf','gbellmf');
MfParams = genparam(data,NumMf,MfType);
set(gcf,'Name','genparam','NumberTitle','off');
NumInput = size(data, 2) - 1;
range = [min(data)' max(data)'];
FirstIndex = [0 cumsum(NumMf)];
for i = 1:NumInput;
subplot(NumInput, 1, i);
x = linspace(range(i, 1), range(i, 2), 100);
index = FirstIndex(i)+1:FirstIndex(i)+NumMf(i);
mf = evalmmf(x, MfParams(index,:), MfType(i,:));
plot(x, mf');
xlabel(['input ' num2str(i) ' (' MfType(i,:) ')']);
end

===================================================================

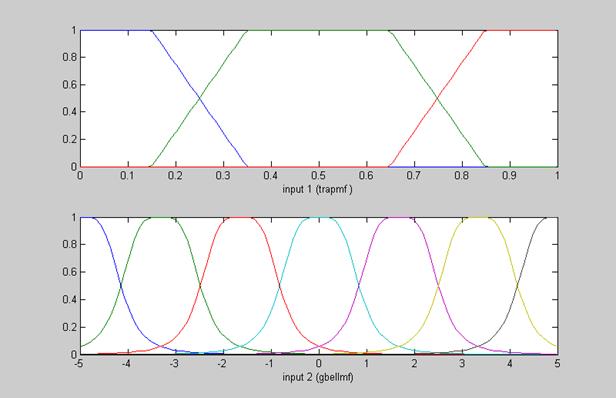
Генерирование трех треугольных и семи колокообразных функций принадлежностей из 1000 пар случайно полученных данных “входы-выход”.

В оглавление \ К следующему разделу \ К предыдущему разделу

GENSURF

Построение поверхности "входы-выход", соответствующей системе нечеткого логического вывода

Синтаксис:

gensurf (fis)
gensurf (fis, inputs, output)
gensurf (fis, inputs, output, grids)
gensurf (fis, inputs, output, grids, refinput)
[x y z] = gensurf(…)

Описание:

Выводит в графическое окно поверхность "входы-выход", которая соответствует системе нечеткого логического вывода. Функция gensurf может иметь до пяти входных аргументов:

1. fis - система нечеткого логического вывода;
2. inputs - вектор, задающий порядковые номера входных переменным системы нечеткого логического вывода, которым будут поставлены в соответствие оси абсцисс и ординат поверхности. Значения по умолчанию - [1 2]. Если задан номер только одной входной переменной, тогда будет построена однофакторная зависимость "вход-выход";
3. output - порядковый номер выходной переменной системы нечеткого логического вывода, которой будет поставлена в соответствие ось аппликат поверхности. По умолчанию выбирается выходная переменная с первым порядковым номером;
4. grids - количество дискрет по осям абсцисс и ординат, необходимых для построения поверхности. Если количество точек одинаково по обеим осям, тогда достаточно указать только одно значение. По умолчанию количество дискрет равно 15;
5. refinput - вектор, задающий значения входных переменных, неассоциированных с координатными осями. Аргумент необходим при количестве входных переменных большем двух. Длина вектора равна количеству входных переменных. Координаты вектора, соответствующие переменным, для которых строится поверхность, должны иметь значения NaN. Остальные координаты вектора refinput фиксируют значения входных неассоциированных с координатными осями переменных. Значения этих координат вектора refinput по умолчанию равны серединам диапазонов изменения соответствующих переменных.

Функция gensurf может иметь три выходных аргумента x, y, z, которые определяют значения входных переменных по осям абсцисс (x) и ординат (y), а также значения выходной переменной (z) в узлах получившийся сетки.

Пример:

a=readfis('tipper')
gensurf(a)

Выводится поверхность "входы - выход" для демонстрационной системы нечеткого логического "Tipper", задающей зависимость размера чаевых от качества пищи и уровня сервиса в ресторане.

В оглавление \ К следующему разделу \ К предыдущему разделу

GETFIS

Получение свойств системы нечеткого логического вывода

Синтаксис:

out = getfis (fis)
out = getfis (fis, fisprop)
out = getfis (fis, vartype, varindex, varprop)
out = getfis (fis, vartype, varindex, 'mf', mfindex, mfprop)

Описание:

Позволяет получить информацию обо всех свойствах системы нечеткого логического вывода. Функция getfis может иметь один, два, четыре или шесть входных аргументов:

1. fis - система нечеткого логического вывода;
2. fisprop - наименование свойства системы нечеткого логического вывода
   Допустимые значения:
   'AggMethod' - реализация операции объединения результирующих нечетких множеств;
   'AndMethod' - реализация логической операции И;
   'DefuzzMethod' - метод дефаззификации;
   'ImpMethod' - реализация импликации;
   'InLabels' - наименования входных переменных;
   'InMfLabels' - термы, используемые для лингвистической оценки выходных переменных;
   'InMfParams' - параметры функций принадлежности входных переменных;
   'InMfs' - количество функций принадлежности входных переменных;
   'InMfTypes' - типы функций принадлежности входных переменных;
   'InRange' - диапазоны изменения входных переменных;
   'Name' - наименование системы нечеткого логического вывода;
   'NumInputMfs' - количество функций принадлежности входных переменных;
   'NumInputs' - количество входных переменных;
   'NumOutMfs' - количество функций принадлежности выходных переменных;
   'NumOutputs' - количество выходных переменных;
   'NumRules' - количество правил в базе знаний;
   'OrMethod' - реализация логической операции ИЛИ;
   'OutLabels' - наименования входных переменных;
   'OutMfLabels' - термы, используемые для лингвистической оценки выходных переменных;
   'OutMfParams' - параметры функций принадлежности выходных переменных;
   'OutMfs' - количество функций принадлежности выходных переменных;
   'OutMfTypes' - типы функций принадлежности выходных переменных;
   'OutRange' - диапазоны изменения выходных переменных;
   'RuleList' - база знаний в индексном формате;
   'Type' - тип системы нечеткого логического вывода (Мамдани или Сугэно);
3. vartype - тип переменной. Допустимые значения: 'input' - входная переменная; 'output' - выходная переменная;
4. varindex - порядковый номер переменной;
5. varprop - наименование свойства переменной.
   Допустимые значения:
   'Name' - наименование переменной;
   'Range' - диапазон изменения переменной;
   'NumMfs' - количество функций принадлежности;
   'MfLabels' - список термов, используемых для лингвистической оценки переменной;
6. mfindex - порядковый номер функции принадлежности переменной;
7. mfprop - наименование свойства функции принадлежности.
   Допустимые значения:
   'Name' - наименование функции принадлежности (терм);
   'Type' - тип функции принадлежности;
   'Params' - параметры функции принадлежности.

Наименования свойств можно задавать в любом регистре.

Пример:

a=readfis('tipper')
out=getfis(a)

Выводится список основных свойств демонстрационной системы нечеткого логического "Tipper".

В оглавление \ К следующему разделу \ К предыдущему разделу

MAM2SUG

Преобразование системы нечеткого логического вывода типа Мамдани в систему типа Сугэно

Синтаксис:

sug_fis=mam2fis(mam_fis)

Описание:

Функция mam2sug преобразовывает систему нечеткого логического вывода типа Мамдани (mam_fis) в систему нечеткого логического вывода типа Сугэно (sug_fis). Система нечеткого логического вывода может иметь несколько входов и выходов. В результате выполнения функции mam2sug получается система типа Сугэно нулевого порядка. Количество правил в системе типа Сугэно остается таким же, как и в исходной системе. Без изменений остаются и "Если"-части правил (посылки), а модифицируются только "То"-части правил (следствия). В "То"-части правил качестве значений выходных переменных используется числовые значения, соответствующие максимуму функций принадлежности выходных переменных в исходной системе.

Пример:

mam_fis=readfis('tipper');
sug_fis=mam2sug(mam_fis);
subplot(1,2,1)
gensurf(mam_fis)
title('Tipper: Mamdani type FIS');
subplot(1,2,2)
gensurf(sug_fis)
title('Tipper: Sugeno type FIS');

Загружается в рабочую область демонстрационная система нечеткого логического "Tipper", задающая зависимость размера чаевых от качества пищи и уровня сервиса в ресторане. С помощью функции mam2sug преобразовывается исходная система типа Мамдани в систему типа Сугэно. На рисунке показаны поверхности "входы - выход" для обеих систем.

В оглавление \ К следующему разделу \ К предыдущему разделу

MF2MF

Пересчет параметров функции принадлежности

Синтаксис:

outParams = mf2mf(inParams, inType, outType)

Описание:

Функция mf2mf позволяет пересчитать параметры одного встроенного типа функции принадлежности в параметры другого типа. Функция mf2mf имеет три входных аргумента:

1. inParams - вектор параметров исходной функции принадлежности;
2. inType - тип исходной функции принадлежности;
3. outType - тип новой функции принадлежности.

Допустимыми значениями типов функций принадлежности: 'trimf'; 'trapmf'; 'pimf'; 'gaussmf'; 'gauss2mf'; 'gbellmf'; 'sigmf'; 'dsigmf'; 'smf'; 'psigmf'; 'zmf'. Описание этих типов функций принадлежности приведено в разделе "Модели функций принадлежности".

Функция mf2mf имеет один выходной аргумент outParams, задающий вектор параметров новой функции принадлежности.

Использование функции mf2mf иногда может привести к некоторому изменению формы функции принадлежности. Например, если полученные параметры функции принадлежности еще раз пересчитать в параметры функции принадлежности исходного типа, то в некоторых случаях обратнопересчитанные параметры не будут равны исходным.

Пример:

x=0:0.1:5;
mfp1 = [1 2 3];
mfp2 = mf2mf(mfp1, 'gbellmf', 'trimf');
plot(x, gbellmf(x, mfp1), x, trimf(x, mfp2))

Пересчет параметров треугольной функции принадлежности в параметры колокообразной функции принадлежности. Последняя строка примера выводит графики треугольной и колокообразной функций принадлежности.

В оглавление \ К следующему разделу \ К предыдущему разделу

NEWFIS

Создание новой системы нечеткого логического вывода

Синтаксис:

fis = newfis(fis_name, fis_type, andMethod, orMethod, impMethod, aggMethod, defuzzMethod)

Описание:

Создает в рабочей области новую систему нечеткого логического вывода. Функция newfis может иметь до семи входных аргументов:

1. fis_name - наименование системы нечеткого логического вывода;
2. fis_type - тип системы нечеткого логического вывода. Допустимые значения:'mamdani' - система типа Мамдани (значение по умолчанию);'Sugeno' - система типа Сугэно;
3. andMethod - реализация логической операции И. Значения по умолчанию: минимум ('min') - для системы типа Мамдани; произведение ('prod') - для системы типа Сугэно;
4. orMethod - реализация логической операции ИЛИ. Значения по умолчанию: максимум ('max') - для системы типа Мамдани; вероятностное ИЛИ ('probor') - для системы типа Сугэно;
5. impMethod - реализация импликации. Значение по умолчанию - 'min' - минимум;
6. aggMethod - реализация операции объединения функций принадлежности выходной переменной. Значение по умолчанию - 'max' - максимум;
7. defuzzMethod - метод дефаззификации. Значения по умолчанию: центр тяжести ('centroid') - для системы типа Мамдани; взвешенное среднее (''wtaver) - для системы типа Сугэно.

Пример:

a=newfis('new_fuzzy_system')

В рабочей области создается структура a, содержащая систему нечеткого логического вывода с именем 'new_fuzzy_system'. Значения всех параметров системы устанавливаются по умолчанию.

В оглавление \ К следующему разделу \ К предыдущему разделу

PARSRULE

Замена правил нечеткой базы знаний

Синтаксис:

outfis = parsrule (infis, inrulelist, ruleformat, lang)
[outfis, outrulelist, errorstr] = parsrule (infis, inrulelist, ruleformat, lang)

Описание:

Функция parsrule предназначена для ввода правил в нечеткую базу знаний. При этом удаляются ранее существующие в базе знаний правила. Функция parsrule может иметь до четырех входных аргументов, первые два из которых обязательные:

1. infis - идентификатор исходной системы нечеткого логического вывода;
2. inrulelist - список правил "если - то". Правила можно задавать в виде предложений на английском, немецком и французских языках, а также в символьном и индексном форматах. Примеры правил в различных форматах приведены в руководстве пользователя по Rule Editor. При задании правил на естественном языке необходимо использовать следующие ключевые слова:
   - для английского языка - "if", "and", "or", "then", "is", "not";
   - для французского языка - "si", "et", "ou", "alors", "est ","n''est_pas";
   - для немецкого языка - "senn", "und", "oder", "dann", "ist", "nicht",
   которые эквиваленты русским словам "если", "и", "или", "то", "есть", "не", соответственно. Весовой коэффициент можно указать в конце правила. По умолчанию значение весового коэффициента равно 1. Список правил задается в виде матрицы, каждая строчка которой определяет одно правило;
3. ruleformat - формат правил. Допустимые значения:
   'verbose' - словесный;
   'symbolic' - символьный;
   'indexed' - индексный.
   Значение по умолчанию - 'verbose'. Примеры представления нечетких правил в различных форматах приведены в разделе 7.3.В формате 'verbose' невозможно в качестве значений переменной использовать терм 'none'. Для задания "коротких" правил необходимо из правила исключить наименования соответствующих переменных;
4. lang - язык представления правил в формате 'verbose'. Допустимые значения:
   'english' - английский;
   'francais' - французский;
   'deutsch' - немецкий.
   По умолчанию установлен английский язык.

Функция parsrule может иметь до трех выходных аргументов:

1. outfis - идентификатор системы нечеткого логического вывода с новыми правилами;
2. outrulelist - список правил системы outfis. Список представляет собой матрицу целых положительных чисел, соответствующих правилам, заданных матрицей inrulelist. Для преобразование чисел в символы необходимо использовать функцию char. Вошедшие в outfis корректно заданные правила в этом списке имеют порядковый номер. Наличие символа '#' указывает на то, что соответствующее правило является некорректным.
3. errorstr - список ошибок задания правил.

Пример:

infis=readfis('tipper');
r1='if service is good then tip is average ';
r2='if service is poor and food is rancid then tip is cheap ';
r3='if service is excellent and food is delicious then tip is generous';
inrulelist=[r1; r2; r3];
outfis=parsrule(infis,inrulelist)

Загружается в рабочую область демонстрационная система нечеткого логического вывода "Tipper", задающая зависимость размера чаевых от качества пищи и уровня сервиса в ресторане. Затем формируется новая база знаний, содержащая следующие правила:

"if service is good then tip is average";
"if service is poor and food is rancid then tip is cheap";
"if service is excellent and food is delicious then tip is generous'".

В оглавление \ К следующему разделу \ К предыдущему разделу

PIMF	Пи-подобная функция принадлежности

Синтаксис:

y = pimf (x, params)

Описание:

Функция pimf задает функцию принадлежности в виде криволинейной трапеции. Эта функция задается как произведение s- и z-подобных функций принадлежности: pimf(x, [a, b, c, d])=smf(x, [a, b]).*zmf(x, [c,d]).

Если b<=c, то параметры функции принадлежности интерпретируются следующим образом:

[a, d] – носитель нечеткого множества;
[b, c] – ядро нечеткого множества.

Когда b>c, нечеткое множество получается субнормальным.

Функция pimf применяется для задания ассиметричных функций принадлежности с плавным переходом от пессиместической к оптимистической оценки нечеткого числа. Функция pimf имеет два входных аргумента:

1. x – вектор, для координат которого необходимо рассчитать степени принадлежности;
2. params – вектор параметров функции принадлежности. Порядок задания параметров – [a b c d].

Функция pimf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x.

Пример:

x = 0: 0.1: 10;
y1 = pimf (x, [0 0.5 3 9]);
y2 = pimf (x, [0 4 5.5 9]);
y3 = pimf (x, [0 6 7 9]);
plot (x, [y1; y2; y3])
title (' pimf, a=0, d=9')
ylim ([0 1.05])
legend (‘b=0.5, c=3’, ‘b=4, c=5,5’, ‘b=6, c=7’)

===================================================================

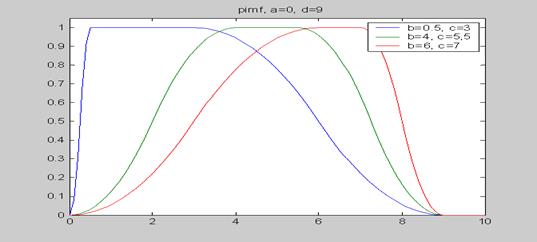
Построение графика пи-подобной функции принадлежности для нечетких множеств с ядрами [0.5, 3], [4, 5.5] и [6, 7].

В оглавление \ К следующему разделу \ К предыдущему разделу

PLOTFIS

Изображение структуры системы нечеткого логического вывода

Синтаксис:

plotfis (fis)

Описание:

Функция plotfis выводит в графическом окне структуру системы нечеткого логического вывода fis. Входные переменные системы изображаются в левой части графического окна, выходные переменные – в правой части, в центре – база знаний. В графическом окне выводится наименование и тип системы нечеткого логического вывода, количество термов для каждой переменной и количество правил. Также изображаются графики функций принадлежности всех термов.

Пример:

a=readfis(‘tipper’);
plotfis(a)

Вывод структуры демонстрационной системы нечеткого логического вывода “Tipper”.

В оглавление \ К следующему разделу \ К предыдущему разделу

PLOTMF

Вывод графиков функций принадлежности термов одной переменной

Синтаксис:

plotmf (fis, varType, varIndex, numPts)
[x, y] = plotmf (fis, varType, varIndex, numPts)

Описание:

Функция plotmf рисуетграфики функций принадлежности термов одной переменной системы нечеткого логического вывода. Функция plotmf может иметь 3 или 4 входных аргумента:

1. fis – система нечеткого логического вывода;
2. varType – тип переменной. Допустимые значения: ‘input' – входная переменная; ‘output' – выходная переменная;
3. varIndex – порядковый номер переменной. Порядковые номера входных и выходных переменных независимы.
4. numPts – количество дискрет, по которым строятся графики функций принадлежности. Значение по умолчанию – 181.

Функция plotmf может иметь два выходных аргумента:

1. x - матрица значений дискрет по оси абцисс для всех графиков функций принадлежности;
2. y - матрица значений функций принадлежности, соответствующих вектору x.

При вызове функции plotmf в формате с выходными аргументами графики функций принадлежности не выводятся.

Пример:

a=readfis(‘tipper’);
plotmf(a, 'input', 1)

В оглавление \ К следующему разделу \ К предыдущему разделу

PROBOR

Вероятностная реализация логической операции ИЛИ

Синтаксис:

y = probor (x)

Описание:

Вероятностная реализация логической операции ИЛИ задается формулой y = a + b – ab. Входной аргумент x представляет собой матрицу степеней принадлежности. Логическая операция ИЛИ выполняется над степенями принадлежностями, записанными в одном столбце матрицы x. Функция probor возвращает вектор y, содержащий результат выполнения логической операции ИЛИ.

Пример:

x = (0:0.1:10);
a = gaussmf(x, [2 4]);
b = gaussmf(x, [1.8 6]);
y = probor([a; b]);
plot (x,[a; b; y])
legend ('a', 'b', 'y=a OR b')
title ('Probabilistic OR')

===================================================================

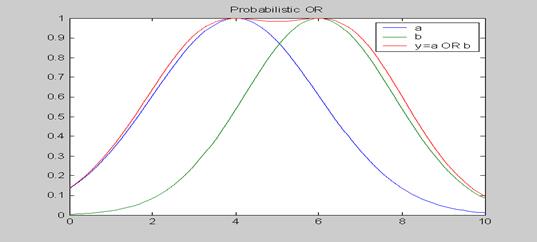
Выполнение операции “вероятностное ИЛИ” над двумя гауссовскими функциями принадлежности с параметрами [2 4] и [1.8 6].

В оглавление \ К следующему разделу \ К предыдущему разделу

PSIGMF

Произведение двух сигмоидных функций принадлежности

Синтаксис:

y = psigmf (x, params)

Описание:

Функция psigmf представляет собой произведение двух сигмоидных функций принадлежности:

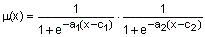
Функция psigmf применяется для задания гладких ассиметричных функций принадлежности. Функция psigmf имеет два входных аргумента:

1. x - вектор, для координат которого необходимо рассчитать степени принадлежности;
2. params - вектор параметров функции принадлежности. Порядок задания параметров - [a1 c1 a2 c2]

Функция psigmf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x.

Пример.

x = 0: 0.1: 10;

y1 = psigmf (x, [2 1 -1 7]);

y2 = psigmf (x, [2 2 -4 7]);

y3 = psigmf (x, [2 3 -8 7]);

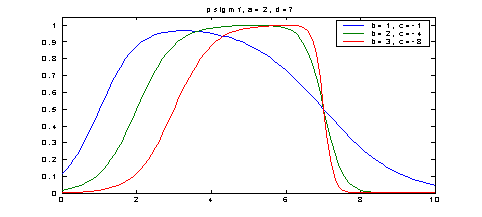
plot (x, [y1; y2; y3])

title (' psigmf, a=2, d=7')

ylim ([0 1.05])

legend ('b=1, c=-1', 'b=2, c=-4', 'b=3, c=-8')

===================================================================

Построение графиков функций принадлежности в виде произведения двух сигмоидных функций

с параметрами [2 1 -1 7], [2 2 -4 7] и [2 3 -8 7].

В оглавление \ К следующему разделу \ К предыдущему разделу

READFIS

Загрузка системы нечеткого логического вывода с диска

Синтаксис:

fis = readfis(‘fisfile’)

Описание:

Загрузка в рабочую область системы нечеткого логического вывода из файла с именем fisfile.fis. Выходным аргументом функции readfis является структура системы нечеткого логического вывода fis.

При вызове функции readfis без входного аргумента появляется типовое окно открытия файла.

Пример:

a=readfis(‘tipper’)

Загружается в рабочую область демонстрационная система нечеткого логического вывода “Tipper”.

В оглавление \ К следующему разделу \ К предыдущему разделу

RMMF	Удаление терма из системы нечеткого логического вывода

Синтаксис:

fis = rmmf (fis, varType, varIndex, ‘mf’, mfIndex)

Описание:

Удаление терма из системы нечеткого логического вывода. Функция rmmf имеет 5 входных аргументов:

1. fis – система нечеткого логического вывода;
2. varType – тип переменной. Допустимые значения: ‘input' – входная переменная; ‘output' – выходная переменная;
3. varIndex – порядковый номер переменной. Порядковые номера входных и выходных переменных независимы;
4. ‘mf’- константа;
5. mfIndex –порядковый номер удаляемого терма, используемого для лингвистической оценки переменной с порядковым номером varIndex.

При попытке удаления терма, используемого в базе знаний, появится окно с запросом на подтверждение удаления.

Пример:

a=readfis(‘tipper’);
b=rmmf(a, ‘input’, 1, ‘mf’, 3)

Удаление терма “excellent” из терм-множества, используемого для лингвистической оценки входной переменной “service” в демонстрационной системе нечеткого логического вывода “Tipper”.

В оглавление \ К следующему разделу \ К предыдущему разделу

RMVAR

Удаление переменной из системы нечеткого логического вывода

Синтаксис:

fis2 = rmvar (fis, varType, varIndex)
[fis2, errorStr] = rmvar (fis, varType, varIndex)

Описание:

Удаление переменной из системы нечеткого логического вывода. Функция rmmf имеет 3 входных аргумента:

1. fis – система нечеткого логического вывода;
2. varType – тип переменной. Допустимые значения: ‘input' – входная переменная; ‘output' – выходная переменная;
3. varIndex – порядковый номер удаляемой переменной. Порядковые номера входных и выходных переменных независимы.

Функция rmmf автоматически модифицирует базу знаний таким образом, чтобы она соответствовала количеству входных и выходных переменных. Перед удалением переменной необходимо из базы знаний исключить все правила, в которых фигурирует данная переменная. В противном случае появится окно с запросом на подтверждение удаления.

Функция rmmf может иметь 2 выходных аргумента:

1. fis2 – система нечеткого логического вывода без переменной с порядковым номером varIndex;
2. errorStr – строка ошибок, возникших во время работы функции.

Пример:

a=readfis(‘tipper’);
b=rmvar(a, ‘input’, 1)

Удаление входной переменной “service” из демонстрационной системы нечеткого логического вывода “Tipper”.

В оглавление \ К следующему разделу \ К предыдущему разделу

SETFIS

Установка свойств системы нечеткого логического вывода

Синтаксис:

fis2 = setfis (fis, fisprop, propvalue)
fis2 = setfis (fis, vartype, varindex, varprop, propvalue)
fis2 = setfis (fis, vartype, varindex, ‘mf’, mfindex, mfprop, propvalue)

Описание:

Позволяет установить свойства системы нечеткого логического вывода. Функция setfis может иметь три, пять или семь входных аргументов:

1. fis – исходная система нечеткого логического вывода;
2. fisprop – наименование свойства системы нечеткого логического вывода, значение которого будет изменено. Допустимые наименования свойств:

‘AggMethod’ – реализация операции объединения результирующих нечетких множеств;
‘AndMethod’ – реализация логической операции И;
‘DefuzzMethod’ – метод дефаззификации;
‘ImpMethod’ – реализация импликации;
‘InLabels’ – наименования входных переменных;
‘InMfParams’ – параметры функций принадлежности входных переменных;
‘Name’ – наименование системы нечеткого логического вывода;
‘OrMethod’ – реализация логической операции ИЛИ;
‘OutLabels’ – наименования входных переменных;
‘OutMfParams’ – параметры функций принадлежности выходных переменных;
‘Type’ – тип системы нечеткого логического вывода (Мамдани или Сугэно);
‘RuleList’ – список правил нечеткой базы знаний;