Четвертая категория программных инструментов пакета Fuzzy Logic Toolbox содержит следующие демонстрационные примеры:
- defuzzdm - дефаззификация различными методами
- fcmdemo - 2D-кластеризация с использование алгоритма fuzzy c-means
- fuzdemos - список всех демонстрационных примеров Fuzzy Logic Toolbox
- gasdemo - применение алгоритма ANFIS и субтрактивной кластеризации для идентификации зависимости топливной эффективности (расход топлива на одну милю) от шести параметров автомобиля
- invkine - инверсная кинематика робота-манипулятора
- irisfcm - применение алгоритма fuzzy c-means для кластеризация ирисов
- juggler - жонглирование шариком с помощью теннисной ракетки с демонстрацией нечеткой базы знаний
- noisedm - адаптивное подавление шумов
- slbb - управление системой “шарик на коромысле” (необходим пакет Simulink)
- slcp - управление системой “перевернутый маятник” (необходим пакет Simulink)
- sltank - управление уровнем воды (необходим пакет Simulink)
- sltankrule - управление уровнем воды с демонстрацией нечеткой базы знаний (необходим пакет Simulink)
- sltbu - парковка грузовика (необходим пакет Simulink)
- mgtsdemo - предсказание временного ряда Маккея-Глэсса
- trips - построение модели прогнозирования количества автомобильных поездок
- shower - управление душем
- slcp1 - перемещение неустойчивой системы "перевернутый маятник переменной длины на тележке" в заданную точку
- slcpp1 - перемещение неустойчивой системы "два перевернутых маятника на тележке" в заданную точку
- slcpp1 - перемещение неустойчивой системы "два перевернутых маятника на тележке" в заданную точку
- mfdemo - вывод на экран окна, содержащего графики всех запрограммированных в Fuzzy Logic Toolbox типов функций принадлежностей
- drydemo - иллюстрирация применения технологии ANFIS для идентификации нелинейных динамических систем на примере процесса нагрева воздуха в фене
| Добавляет функцию принадлежности к системе нечеткого логического вывода
|
Синтаксис:
FIS_name=addmf(FIS_name, varType, varIndex, mfName, mfType, mfParams)
Описание:
Функцию принадлежности можно добавить только к существующей в рабочей области MatLab системе нечеткого логического вывода. Другими словами система нечеткого логического вывода должна быть каким-то образом загружена в рабочую область или создана с помощью функции newfis. Функция addmf имеет шесть входных аргументов:
- FIS_name – идентификатор системы нечеткого логического вывода в рабочей области MatLab;
- varType – тип переменной, к которой добавляется функция принадлежности. Допустимые значения - ‘input’ - входная переменная и ‘output’ – выходная переменная;
- varIndex – порядковый номер переменной, к которой добавляется функция принадлежности;
- mfName – наименование добавляемой функции принадлежности (терм). Задается в виде строки символов;
- mfType – тип (модель) добавляемой функции принадлежности. Задается в виде строки символов;
- mfParams – вектор параметров добавляемой функции принадлежности.
Порядковый номер функции принадлежности в системе нечеткого логического вывода соответствует порядку добавления с помощью функции addmf, т.е. первая добавленная функция принадлежности всегда будет иметь порядковый номер 1. С помощью функции addmf невозможно добавить функцию принадлежности к несуществующей переменной. В этом случае необходимо вначале добавить переменную к системе нечеткого логического вывода с помощью функции addvar.
Пример.
FIS_name=addmf(FIS_name, ‘input’, 1, ‘низкий’, ‘trapmf’, [150, 155, 165, 170])
Строка добавляет в терм-множество первой входной переменной нечеткой системы FIS_name терм ‘низкий’ с трапециевидной функцией принадлежности с параметрами [150, 155, 165, 170].
В оглавление \ К следующему разделу \ К предыдущему разделу
| Добавляет правила в базу знаний системы нечеткого логического вывода
|
Синтаксис:
FIS_name= addrule (FIS_name, ruleList)
Описание:
Правила можно добавить только к существующей в рабочей области MatLab системе нечеткого логического вывода. Функция addrule имеет два входных аргумента:
- FIS_name – идентификатор системы нечеткого логического вывода в рабочей области MatLab;
- ruleList – матрица добавляемых правил.
Матрица правил должна быть задана в формате indexed. Количество строк матрицы ruleList равно количеству добавляемых правил, т.е. каждая строка матрицы соответствует одному правилу. Количество столбцов матрицы равно m+n+2, где m (n) – количество входных (выходных) переменных системы нечеткого логического вывода.
Первые m столбцов соответствуют входным переменным, т.е. задают ЕСЛИ-часть правил. Элементы этих столбцов содержат порядковые номера термов, используемых для лингвистической оценки соответствующих входных переменных. Значение 0 указывает, что соответствующая переменная в правиле не задана, т.е. ее значение равно none.
Следующие n столбцов соответствуют выходным переменным, т.е. задают ТО-часть правил. Элементы этих столбцов содержат порядковые номера термов, используемых для лингвистической оценки соответствующих выходных переменных.
Предпоследний столбец матрицы содержит весовые коэффициенты правил. Значения весовых коэффициентов должны быть в диапазоне [0, 1].
Последний столбец матрицы задает логические связки между переменными внутри правил. Значение 1 соответствует логической операции И, а значение 2 – логической операции ИЛИ.
Пример.
FIS_name=addrule(FIS_name, [1 1 1 1 1; 1 2 2 0.5 1])
Строка добавляет в базу знаний системы FIS_name два правила, которые интерпретируются следующим образом:
Если вход1=MF1 и вход2=MF1, то выход1=MF1 с весом 1,
Если вход1=MF1 и вход2=MF2, то выход1=MF2 с весом 0.5,
где MF1 (MF2) – терм с порядковым номером 1 (2).
В оглавление \ К следующему разделу \ К предыдущему разделу
| Добавляет переменную в систему нечеткого логического вывода
|
Синтаксис:
FIS_name= addvar (FIS_name, varType, varName, varBound)
Описание:
Переменную можно добавить только к существующей в рабочей области MatLab системе нечеткого логического вывода. Функция addrvar имеет четыре входных аргумента:
- FIS_name – идентификатор системы нечеткого логического вывода в рабочей области MatLab;
- varType – тип добавляемой переменной. Допустимые значения - ‘input’ - входная переменная и ‘output’ – выходная переменная;
- varName – наименование добавляемой переменной. Задается в виде строки символов;
- varBound – вектор, задающий диапазон изменения добавляемой переменной.
Порядковый номер переменной в системе нечеткого логического вывода соответствует порядку добавления с помощью функции addvar, т.е. первая добавленная переменная будет иметь порядковый номер 1. Входные и выходные переменные нумеруются независимо.
Пример.
FIS_name=addrule(FIS_name, ‘input’, ‘Рост’, [155 205])
Строка добавляет в систему нечеткого логического вывода FIS_name входную переменную ‘Рост’, заданную на интервале [155 205].
В оглавление \ К следующему разделу \ К предыдущему разделу
| Настройка систем нечеткого логического вывода типа Сугэно
|
Синтаксис:
[fis, error] = anfis(trndata)
[fis, error] = anfis(trndata, initfis)
[fis, error, stepsize] = anfis(trndata, initfis, trnopt, dispopt, [], optmethod)
[fis, error, stepsize, chkfis, chkerror] = anfis(trndata, initfis, trnopt, dispopt, chkdata)
Описание:
ANFIS является аббревиатурой Adaptive Network – based Fuzzy Inference System. Это основная функция настройки систем нечеткого логического вывода типа Сугэно. Настройка представляет собой итерационную процедуру нахождения таких параметров системы нечеткого логического вывода, в частности параметров функций принадлежности, которые минимизируют расхождения между результатами логического вывода и экспериментальными данными, т. е. между действительным и желаемым поведениями системы. Экспериментальные данные, по которым настраивается функции принадлежности, представляются в виде обучающей выборки.
В основу функции anfis положен один из первых методов построения нейро-нечетких систем для аппроксимации функций, предложенный в 1991 году Янгом (Jang). Для идентификации параметров системы нечеткого логического вывода типа Сугэно функция anfis может использовать метод обратного распространения ошибки а также гибридный алгоритм, основанный на комбинации метода обратного распространения ошибки и метода наименьших квадратов. Функция anfis может использовать дополнительный аргумент для проверки модели – тестирующую выборку.
Функция anfis может имеет шесть входных аргументов:
- trndata – идентификатор обучающей выборки. Этот входной аргумент является обязательным. Обучающая выборка представляет собой матрицу, каждая строчка которой является парой “входы-выход”. Последний столбец матрицы соответствует вектору значений выхода, а все остальные столбцы – входным данным. Заметим, что функцию anfis можно использовать для проектирования систем типа SISO (один вход - один выход) и типа MISO (много входов – один выход);
- initfis – идентификатор исходной системы нечеткого логического вывода, функции принадлежности которой будут настроены с помощью anfis. Исходная система нечеткого логического вывода должна быть системой типа Сугэно нулевого или первого порядка. Еще одним ограничением anfis является недопустимым использования типов функций принадлежностей и методов дефаззификации, определяемых пользователем. При отсутствии аргумента initfis функция anfis вызовет функцию genfis1, которая генерирует типовую систему нечеткого логического вывода. Эта типовая система будет использовать по две функции принадлежности гауссовского типа для каждой входной переменной. В случае, когда пользователь хочет получить систему с иным количеством функций принадлежности, необходимо задать в виде аргумента initfis количество функций принадлежности для оценки каждой входной переменной. Если количество функций принадлежности одинаково для всех входов, тогда достаточно указать только одно значение.
- trnopt – вектор параметров настройки:
trnopt(1) – количество итераций (значение по умолчанию – 10);
trnopt(2) – допустимая ошибка обучения (значение по умолчанию – 0);
trnopt(3) – исходная длина шага (значение по умолчанию – 0.01);
trnopt(4) – коэффициент уменьшения длины шага (значение по умолчанию – 0.9);
trnopt(5) – коэффициент увеличения длины шага (значение по умолчанию – 1.1);
- dispopt – вектор, указывающий какие промежуточные результаты обучения выводить в командное окно MatLab во время настройки. Для вывода информации на экран необходимо установить соответствующую координату вектора в 1. Вектор dispopt имеет четыре координаты:
dispopt(1) – ANFIS-информация: количество функций принадлежности входных и выходной переменных и т.п.;
dispopt(2) – ошибка обучения;
dispopt(3) – длина шага, (выводится в случае его изменения);
dispopt(4) – окончательный результат.
По умолчанию значения всех координат равны 1;
- chkdata – идентификатор тестирующей выборки. Тестирующая выборка используется для исследования свойства обобщения системы нечеткого логического вывода, т. е. способности системы выдавать правильные результаты для данных, отсутствующих в обучающей выборке. Формат тестирующей выборки такой же как и обучающей. Обычно элементы тестирующей выборки несколько отличаются от элементов обучающей выборки. Тестирующая выборка особенно важна для задач обучения с большим количеством входов и (или) для задач с зашумленными данными. При формировании обучающей и тестирующей выборок необходимо стремится к обеспечению свойств представительности выборок;
- optmethod – метод оптимизации, используемый для настройки. Допустимые значения: 1 – гибридный алгоритм и 0 – метод обратного распространения ошибки. По умолчанию применяется гибридный алгоритм, который использует метод обратного распространения ошибки (метод наискорейшего спуска) для настройки функций принадлежности входных переменных и метод наименьших квадратов для настройки функций принадлежности выхода. Точнее говоря, метод наименьших квадратов используется для нахождения коэффициентов линейных функций, связывающих входы и выход в каждом правиле. Метод по умолчанию используется всегда, за исключением случая, когда значение аргумента optmethod равно 0.
Функция anfis может имеет пять выходных аргументов:
- fis – система нечеткого логического вывода, параметры которой настроены таким образом, что минимизируют расхождения между результатами логического вывода и экспериментальными данными из обучающей выборки;
- error – вектор, содержащий значения ошибки обучения на каждой итерации. Ошибка обучения рассчитывается как среднее квадратическое отклонение между результатами нечеткого логического вывода и значениями выходной переменной из обучающей выборки;
- stepsize – вектор, содержащий значения длины шага алгоритма оптимизации на каждой итерации;
- chkfis – система нечеткого логического вывода, параметры которой настроены таким образом, что минимизируют расхождения между результатами логического вывода и экспериментальными данными из тестирующей выборки. Для получения такой системы необходимо задать пятый входной аргумент функции anfis – тестирующую выборку;
- chkerror - вектор, содержащий значения ошибки тестирования на каждой итерации. Ошибка тестирования рассчитывается как среднее квадратическое отклонение между результатами нечеткого логического вывода и значениями выходной переменной из тестирующей выборки. Для расчета ошибки тестирования необходимо задать пятый входной аргумент функции anfis – тестирующую выборку.
Процесс настройки прекращается по достижению требуемой ошибки обучения настройки или после выполнения указанного количества итераций.
Функция anfis может быть вызвана с одним входным аргументом – обучающей выборкой и одним выходным аргументом – системой нечеткого логического вывода, параметры которой настроены по обучающей выборке. При вызове функции anfis значения неинициализированых аргументов принимаются равными по умолчанию. При инициализации только части аргументов, например, первого и шестого – обучающей и тестирующей выборок, значения остальных аргументов (для нашего примера - второго, третьего, четвертого и пятого) необходимо задать как [] или NaN. Значение [] или NaN указывает, что соответствующий аргумент принимает значения, установленные по умолчанию. Значения, установленные по умолчанию могут быть изменены путем непосредственного редактирования файла anfis.m.
Пример.
Синтезируется и настраивается система нечеткого логического вывода fis, моделирующая зависимость y=sin(x) в диапазоне [0, 1].
x=(0:0.04:1)’;
y=sin(x);
trndata=[x y];
[fis, error, stepsize]=anfis(trndata)
В оглавление \ К следующему разделу \ К предыдущему разделу
| Преобразовывает систему нечеткого логического вывода, заданную в формате Fuzzy Logic Toolbox v.1 в формат Fuzzy Logic Toolbox v.2
|
Синтаксис:
FIS_new= convertis (FIS_old)
Описание:
Функция преобразовывает систему нечеткого логического, заданную матрицей FIS_old в формате Fuzzy Logic Toolbox v.1 в структуру FIS_new, в соответствии с форматом Fuzzy Logic Toolbox v.2.
В оглавление \ К следующему разделу \ К предыдущему разделу
| Дефаззификация нечеткого множества
|
Синтаксис:
crisp = defuzz (x, mf, method)
Описание:
Выполняет операцию дефаззификации, т. е. преобразование нечеткого множества в четкое число. Функция defuzz имеет три входных аргумента:
- x – универсальное множество, на котором задано нечеткое множество, подлежащее дефаззификации;
- mf – вектор степеней принадлежности элементов множества x нечеткому множеству, подлежащему дефаззификации;
- method – метод дефаззификации. Допустимые значения:
‘centroid’ – центр тяжести;
‘bisector’ – медиана;
‘mom’ – центр максимумов;
‘som’ - наименьший из максимумов;
‘lom’ - наибольший из максимумов.
Более подробно методы дефаззфикации описаны в разделе 1. Если метод дефаззификации отличается от вышеуказанных, тогда он должен быть представлен в виде m-функции. В этом случае значения аргументов x и mf будут переданы этой функции для выполнения дефаззификации.
Пример.
Проводится дефаззификация нечеткого множества с трапециевидной функцией принадлежности с параметрами [0, 2, 4, 10]);, заданного на универсальном множестве {0, 0.1, 0.2,…,10}.
x=0:0.1:10’;
mf=trapmf(x, [0, 2, 4, 10]);
crisp=defuzz(x, mf, ‘centroid’)
В оглавление \ К следующему разделу \ К предыдущему разделу
| Дискретизация функций принадлежности всех термов, входящих в систему нечеткого логического вывода
|
Синтаксис:
[XI, YI, XO, YO, R] = discfis (fis, numPts)
Описание:
Функция используется для ускорения нечеткого логического вывода путем дискретизации функций принадлежности всех термов, входящих в систему нечеткого логического вывода. Функция discfis иметь два входных аргумента:
- fis – система нечеткого логического вывода;
- numPts – необязательный входной аргумент, задающий количество точек дискретизации функций принадлежности. Значение по умолчанию равно 181. Это означает, что все нечеткие множества представляются в виде 181 пары чисел “элемент универсального множества – степень принадлежности”. При уменьшении точек дискретизации возрастает скорость выполнения логического вывода и уменьшается точность вычислений, и наоборот.
Функция discfis возвращает 5 выходных аргументов:
- XI – матрица абцисс-координат функций принадлежностей термов входных переменных. Размер матрицы numPts x Ninp, где Ninp – количество термов, используемых для лингвистической оценки входных переменных;
- YI – матрица степеней принадлежности элементов матрицы XI соответствующим термам. Размер матрицы numPts x Ninp, причем первый столбец содержит степени принадлежности первому терму первой входной переменной, а последний – последнему терму последней входной переменной;
- XO – матрица абцисс-координат функций принадлежности термов выходных переменных. Размер матрицы numPts x Nout, где Nout – количество термов, используемых для лингвистической оценки выходных переменных;
- YO – матрица степеней принадлежности элементов матрицы XO соответствующим термам. Размер матрицы numPts x Nout, причем первый столбец содержит степени принадлежности первому терму первой выходной переменной, а последний – последнему терму последней выходной переменной. Для системы типа Сугэно матрица YO является нулевой;
- R – список правил базы знаний в индексном формате.
Пример:
fis = readfis (‘tipper’);
[XI, YI, XO, YO, R] = discfis (fis)
===================================================================
Дискретизация функций принадлежностей демонстрационной системы нечеткого логического вывода “Tipper”.
В оглавление \ К следующему разделу \ К предыдущему разделу
| Функция принадлежности в виде разности между двумя сигмоидными функциями
|
Синтаксис:
y = dsigmf(x, params)
Описание:
Функция принадлежности в виде разности между двумя сигмоидными функциями задается формулой  . Применяется для задания гладних ассиметричных функций принадлежности.
. Применяется для задания гладних ассиметричных функций принадлежности.
Функция dsigmf имеет два входных аргумента:
- x – вектор, для координат которого необходимо рассчитать степени принадлежности;
- params – вектор параметров функции принадлежности. Порядок задания параметров – [a1 c1 a2 c2].
Функция dsigmf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x.
Пример:
x = 0: 0.1: 10;
y1 = dsigmf (x, [5 1 8 7]);
y2 = dsigmf (x, [5 4 5 7]);
y3 = dsigmf (x, [5 6 2 7]);
plot (x, [y1; y2; y3])
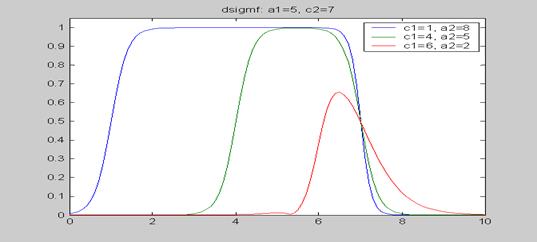
title ('dsigmf: a1=5, c2=7')
ylim([0 1.05])
legend(‘c1=1, a2=8’, ‘c1=4, a2=5’, ‘c1=6, a2=2’)
===================================================================
Построение графиков функций принадлежности в виде разности между двумя сигмоидными функциями с разными параметрами на интервале [0, 10].
В оглавление \ К следующему разделу \ К предыдущему разделу
| Выполнение нечеткого логического вывода
|
Синтаксис:
output = evalfis(input, fis)
output = evalfis(input, fis, numPts)
[output, IRR, ORR, ARR] = evalfis(input, fis)
[output, IRR, ORR, ARR] = evalfis(input, fis,, numPts)
Описание:
Выполняет нечеткий логический вывод. Функция evalfis может иметь три входных аргумента, первые два из которых обязательные:
- input – матрица значений входных переменных, для которых необходимо выполнить нечеткий логический вывод. Матрица должна иметь размер M x N, где N – количество входных переменных; M – количество входных данных. Каждая строчка матрицы представляет один вектор значений входных переменных;
- fis – идентификатор системы нечеткого логического вывода;
- numPts – необязательный входной аргумент, задающий количество точек дискретизации функций принадлежности. Значение по умолчанию равно 101. Это означает, что все нечеткие множества представляются в виде 101 пары чисел “элемент универсального множества – степень принадлежности”. При уменьшении точек дискретизации возрастает скорость выполнения логического вывода и уменьшается точность вычислений, и наоборот.
Функция evalfis может иметь четыре выходных аргумента:
- output – матрица значений выходных переменных, получаемая в результате нечеткого логического вывода для вектора входных значений input. Матрица имеет размер M x L, где M – количество входных данных; L – количество выходных переменных в fis;
- IRR – матрица размером NR x N, где NR – количество правил в fis; N – количество входных переменных. Матрица содержит степени принадлежности входных значений термам, входящих в базу знаний;
- ORR – матрица размером numPts x (NR*L), где numPts – количество точек дискретизации; NR – количество правил в fis; L – количество выходных переменных в fis. Каждый столбец матрицы содержит функцию принадлежности выходной переменной, получаемую в результате вывода по одному правилу. Функция принадлежности дискретизируется на numPts точках и представляется в виде множества степеней принадлежности;
- ARR – матрица размером numPts x L, где numPts – количество точек дискретизации; L – количество выходных переменных в fis. Матрица содержит функции принадлежности выходных переменных, получаемые в результате нечеткого логического вывода по всей базе знаний. Функции принадлежности дискретизируются на numPts точках и представляются в виде множества степеней принадлежности.
Аргументы IRR, ORR и ARR являются необязательными, они содержат промежуточные результаты нечеткого логического вывода. В случае задания нескольких входных данных значения аргументов IRR, ORR и ARR будут рассчитаны только для последнего вектора входных данных. Эти аргументы используются когда необходимо отследить процесс логического вывода или когда необходимо реализовать нестандартную процедуру нечеткого вывода.
Пример.
Первая строчка загружает демо-систему нечеткого логического вывода tipper, предназначенную для определения процента чаевых в ресторане. Вторая строчка рассчитывает размер чаевых, в случае если service=3 и food=8.
fis = readfis('tipper');
tip = evalfis([3 8], fis)
В оглавление \ К следующему разделу \ К предыдущему разделу
| Вычисление значений произвольной функции принадлежности
|
Синтаксис:
y = evalmf (x, params, type)
Описание:
Позволяет вычислить значения произвольной функции принадлежности Функция evalmf иметь три входных аргумента:
- x – вектор, для координат которого необходимо рассчитать степени принадлежности;
- params – вектор параметров функции принадлежности, порядок задания которых определяется ее типом;
- type – тип функции принадлежности. Значение типа функции принадлежности может быть задано в виде строчки символов или числом:
1 - 'trimf';
2 - 'trapmf';
3 - 'gaussmf';
4 – ‘gauss2mf';
5 - 'sigmf';
6 - 'dsigmf';
7 - 'psigmf';
8 - 'gbellmf';
9 - 'smf';
10 - 'zmf';
11 - 'pimf'.
При задании другого типа функции принадлежности предполагается, что она определена пользователем и задана соответствующим m-файлом.
Функция evalmf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x.
Пример:
x = 0: 0.1: 10;y = evalmf (x, [0 3 9], 1);plot (x, y)title (‘Triangular membership function with parameters [0 3 9]')
===================================================================
Построение графика треугольной функции принадлежности с параметрами [0 3 9] на интервале [0, 10].

В оглавление \ К следующему разделу \ К предыдущему разделу
| Вычисление степеней принадлежностей для нескольких функций принадлежностей
|
Синтаксис:
y = evalmmf (x, params, types)
Описание:
Позволяет вычислить значения нескольких функции принадлежности нечетких множеств, заданных на одном и том же универсальном множестве. Функция evalmmf иметь три входных аргумента:
- x – вектор, для координат которого необходимо рассчитать степени принадлежности;
- params – матрица параметров функции принадлежности. Первая строка матрицы определяет параметры первой функции принадлежности, вторая строка – параметры второй функции принадлежности и т.д.;
- types – матрица типов функции принадлежности. Первая строка матрицы задает тип первой функции принадлежности, вторая строка – тип второй функции принадлежности и т.д. Значение типа функции принадлежности может быть задано в виде строчки символов или числом: 1 - 'trimf'; 2 - 'trapmf'; 3 - 'gaussmf'; 4 – ‘gauss2mf'; 5 - 'sigmf'; 6 - 'dsigmf'; 7 - 'psigmf'; 8 - 'gbellmf'; 9 - 'smf'; 10 - 'zmf'; 11 - 'pimf'. При задании другого типа функции принадлежности предполагается, что она определена пользователем и задана соответствующим m-файлом.
Функция evalmmf возвращает матрицу y, содержащую степени принадлежности координат вектора x. Первая строка матрицы содержит значения первой функции принадлежности, вторая строка – значения второй функции принадлежности и т.д.
Пример:
x = 0:0.2:10;para = [-1 2 3 4; 3 4 5 7; 5 7 8 0; 2 9 0 0];type = str2mat('pimf', 'trapmf', 'trimf', 'sigmf');mf = evalmmf(x, para, type);
plot(x', mf');
ylim([0 1.05])
legend('pimf', 'trapmf', 'trimf', 'sigmf');
===================================================================

 . Применяется для задания гладних ассиметричных функций принадлежности.
. Применяется для задания гладних ассиметричных функций принадлежности.




