Демонстрационные примеры 4 страница
‘Name’ – наименование переменной;
‘Name’ – наименование функции принадлежности (терм); Пример: fis = readfis (‘tipper’); Установка метода дефаззификации “средний из максимумов” в демонстрационной системе нечеткого логического вывода “Tipper”. Наименования свойств можно задавать в любом регистре. Функция setfis возвращает систему нечеткого логического вывода fis2 с новым значением соответствующего свойства. В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: showfis (fis) Описание: Функция showfis выводит на экран рабочей области значения следующих свойств системы нечеткого логического вывода fis: Name – наименование системы нечеткого логического вывода; Пример: fis = readfis (‘tipper’); Вывод на экран значений свойств демонстрационной системы нечеткого логического вывода “Tipper”. В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: outStr = showrule (fis, ruleIndex, ruleFormat, lang) Описание: Функция showrule возвращает переменную outStr, содержащую список правил базы знаний системы нечеткого логического вывода fis. Если выходной аргумент функции не задан, то список правил выводится на экран рабочей области. Функция showrule может иметь до четырех входных аргументов:
‘verbose’ – словесный;
'english' – английский; Пример: fis = readfis (‘tipper’); Вывод на экран списка правил базы знаний демонстрационной системы нечеткого логического вывода “Tipper”. В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: y = sigmf (x, params) Описание: Сигмоидная функция принадлежности задается формулой a – коэффициент крутизны функции принадлежности; Функция sigmf применяется для задания монотоных функций принадлежности. Функция sigmf имеет два входных аргумента:
Функция sigmf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x. Пример: x = 0: 0.1: 10; =================================================================== Построение графиков сигмоидных функций принадлежности с различными коэффициентами крутизны на интервале [0, 10].
В оглавление \ К следующему разделу \ К предыдущему разделу
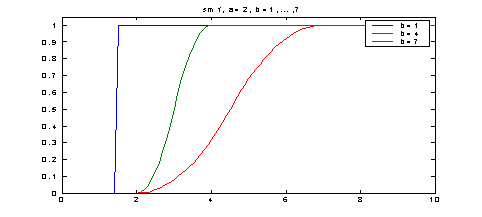
Синтаксис: y = smf (x) Описание: Функция smf задает S-подобную двухпараметрическую функцию принадлежности. Это неубывающая функция принадлежности, принимающая значения от 0 до 1. Параметры функции принадлежности опеределяют интервал, внутри которого функция нелинейно возрастает от 0 до 1. Функция smf применяется для представления нечетких множеств типа "очень высокий", т.е. для задания неубывающих функций принадлежности с насыщением. Функция smf имеет два входных аргумента:
Функция smf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x. Пример. x = 0: 0.1: 10; y1 = smf (x, [2 1]); y2 = smf (x, [2 4]); y3 = smf (x, [2 7]); plot (x, [y1; y2; y3]) title (' smf, a=2, b=1,…,7') ylim ([0 1.05]) legend ('b=1', 'b=4', 'b=7') =================================================================== Построение графиков s-подобных функций принадлежности функций с параметрами [2 1], [2 4] и [2 7].
В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: [centers, sigmas] = subclust (X, radii, xBounds, options) Описание: На основе субтрактивного алгоритма вычисляются центры кластеров данных. Основу алгоритма, реализованного функцией subclust, составляют идеи горного метода кластерного анализа, который был предложен Рональдом Ягером (Ronald Yager) и Димитаром Филевым (Dimitar Filev). Особенностью метода является отсутствие необходимости задания количества кластеров до начала работы алгоритма. Задача нахождения центров кластеров ставится следующим образом. Дано: Идея метода заключается в следующем. Объекты рассматриваются как потенциальные центры кластеров. Для каждого объекта рассчитывается значение так называемого потенциала, характеризующего плотность расположения других объектов в его окрестности. Чем гуще соседние объекты расположены к данному объекту, тем больше значение его потенциала. Значение потенциала для объекта Функция subclust может иметь до четырех входных аргументов, первые два из которых обязательны:
Функция subclust может иметь до двух выходных аргументов:
Если функция subclust вызывается без выходных аргументов, тогда координаты центров кластеров выводятся на экран. Пример: data=load('clusterdemo.dat'); Кластерный анализ данных, записанных в демонстрационном файле clusterdemo.dat. Красными звездочками указаны центры найденных кластеров.
В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: out = sugmax(fis) Описание: Функция sugmax находит диапазон изменения выходных переменных системы нечткого логического вывода типа Сугено, заданной аргументом fis. Каждая строка матрицы out соответствует одной выходной переменной. В первом столбце матрицы записываются минимально возможные значения выходных переменных, а во втором – максимально возможные значения. Пример: fis = readfis ('juggler'); out= sugmax (fis) =================================================================== Нахождения диапазона изменения выходной переменной демонстрационной системы нечеткого логического вывода ‘juggler’. В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: y = trapmf (x, params) Описание: Функция trapmf задает функцию принадлежности в форме трапеции. Трапециевидная функция принадлежности задается следующей аналитической формулой Параметры трапециевидной функции принадлежности интерпретируются так: [a, d] – носитель нечеткого множества - пессимистическая оценка значений переменной; Функция trapmf применяется для задания ассиметричных функций принадлежности переменных, наиболее возможные значения которых принимаются на некотором интервле. Функция trapmf имеет два входных аргумента:
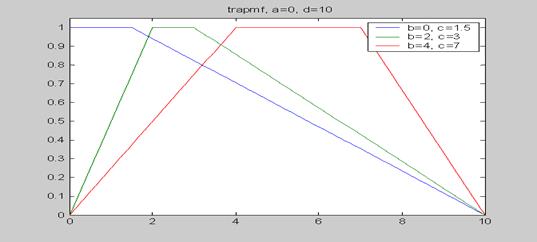
Функция trapmf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x. Пример: x = 0: 0.1: 10; =================================================================== Построение графиков трапециевидных функций принадлежности с параметрами [0 0 1.5 10], [0 2 3 10] и [0 4 7 10].
В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: y = trimf (x, params) Описание: Функция trimf задает функцию принадлежности в форме треугольника. Эта простая и наиболее часто применяемая функция принадлежности. Треугольная функция принадлежности задается следующей аналитической формулой Параметры треугольной функции принадлежности обычно интерпретируются так: [a, c] – диапазон изменения переменной; Функция trimf имеет два входных аргумента:
Функция trimf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x. Пример: x = 0: 0.1: 10; =================================================================== Построение графиков треугольных функций принадлежности с параметрами [0 0 10], [0 3 10] и [0 7 10]. В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: writefis (fis, filename, 'dialog') Описание: Функция writefis сохраняет систему нечеткого логического вывода на диске. Функция writefis может иметь до трех входных аргументов:
При вызове функции writefis с одним аргументом будет открыто типовое диалоговое окно записи файла на диск. Однако, в отличие от вызова функции с тремя аргументами, имя файла по умолчанию в этом окне установлено не будет. При вызове функции writefis с двумя аргументами диалоговое окно записи файла на диск не появится. Система будет сохранена в текущей папке. Расширение “.fis” будет добавлено к имени файла в случае, если это расширение не было задано аргументом filename. Пример: fis = readfis (‘tipper’); Запись демонстрационной системы нечеткого логического вывода “Tipper” в файл с именем “tipper_copy.fis”. В оглавление \ К следующему разделу \ К предыдущему разделу
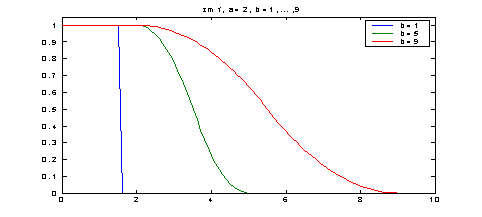
Синтаксис: y = zmf (x, params) Описание: Функция zmf задает Z-подобную двухпараметрическую функцию принадлежности. Это невозрастающая функция принадлежности, принимающая значения от 1 до 0. Параметры функции принадлежности опеределяют интервал, внутри которого функция нелинейно убывает от 0 до 1. Функция zmf применяется для представления нечетких множеств типа "очень низкий", т.е. для задания невозрастающих функций принадлежности с насыщением. Функция zmf имеет два входных аргумента:
Функция zmf возвращает выходной аргумент y, содержащий степени принадлежности координат вектора x. Пример. x = 0: 0.1: 10; y1 = zmf (x, [2 1]); y2 = zmf (x, [2 5]); y3 = zmf (x, [2 9]); plot (x, [y1; y2; y3]) title (' zmf, a=2, b=1,…,9') ylim ([0 1.05]) legend ('b=1', 'b=5', 'b=9') =================================================================== Построение графиков s-подобных функций принадлежности функций с параметрами [2 1], [2 5] и [2 9].
В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис: fuzblock Описание: Библиотека содержит следующие блоки:
Для включения системы нечеткого логического вывода в Simulink-модуль необходимо выбрать блок Fuzzy Logic Controller или Fuzzy Logic Controller with Ruleviewer, затем сделать двойной щелчок по этому блоку и в появившимся диалоговом окне ввести имя файла или наименование переменной в рабочей области, соответствующим системе нечеткого логического вывода. Если система нечеткого логического вывода имеет несколько входов, тогда в Simulink-модуле эти входы необходимо мультиплексировать вместе до ввода в нечеткий контроллер. Аналогично, если система нечеткого логического вывода имеет несколько выходов, тогда выходные сигналы блока будут представлены одной мультиплексной линией. Для построения нетиповых нечетких контроллеров, т. е. отличных от блоков Fuzzy Logic Controller и Fuzzy Logic Controller with Ruleviewer. можно использовать блоки, входящие в библиотеку функций принадлежности (Membership Functions):
В оглавление \ К следующему разделу \ К предыдущему разделу
Синтаксис output = sffis (t, x, u, flag, fis) Описание Функция sffis - это MEX-файл, специально оптимизированный для использования в пакете Simulink. Функция sffis выполняет нечеткий логический вывод аналогично функции evalfis. Функция sffis имеет 5 входных аргументов:
Функция sffis возвращает единственный аргумент output, содержащий результат нечеткого логического вывода.
Описание: В этом разделе описывается демонстрационная программа defuzzdm, иллюстрирующая применение следующих встроенных методов дефаззификации:
Наиболее часто применяемым методом дефаззификации является центр тяжести. Однако, применяя этот метод необходимо помнить, что диапазон четких (после дефаззификации) значений выходной переменной будет всегда уже интервала, на котором она определена. Этого недостатка лишен второй по частоте использования метод дефаззификации - центр максимумов. При использовании метода центра максимумов следует учитывать то, что результат дефаззификации не чувствителен к вкладу правил, степени выполнения которых малы, т.к. он зависит лишь от правил, степени выполнения которых максимальны. Во многих случаях существует только одно такое правило, которое и определяет результат нечеткого логического вывода. Программа defuzzdm выводит на экран графическое окно (рис. 1.), содержащее результаты дефаззификации для двух нечетких чисел - положительного и отрицательного.
Рисунок 1. – Дефаззификация различными методами В оглавление \ К следующему разделу \ К предыдущему разделу
Описание: В этом разделе описывается демонстрационная программа fcmdemo, иллюстрирующая применение нечеткого c-means алгоритма для задач кластеризации. Программа fcmdemo выводит на экран интерактивное графическое окно, позволяющее пользователю выбирать набор данных для кластеризации. устанавливать параметры нечеткого c-means алгоритма, просматривать результаты кластеризации, в том числе и графики функций принадлежности центров кластеров. Во время кластерного анализа в рабочую область MatLab выводятся значения целевой функции на каждой итерации нечеткого c-means алгоритма. Графическое окно fcmdemo суказанием функционального назначения основных полей приведено на рис. 1.
Рисунок 1. – Окно демонстрационной программы fcmdemo Графическое окно fcmdemo содержит 7 верхних типовых меню (File, Edit, View, Insert, Tools, Windows и Help), область визуализации, меню выбора данных, меню установки параметров алгоритма кластеризации, кнопку запуска кластерного анализа (Start), а также кнопки Info и Close, которые позволяют вызвать окно справки и закрыть модуль, соответственно.
|

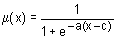 , параметры которой геометрически интерпретируются следующим образом:
, параметры которой геометрически интерпретируются следующим образом: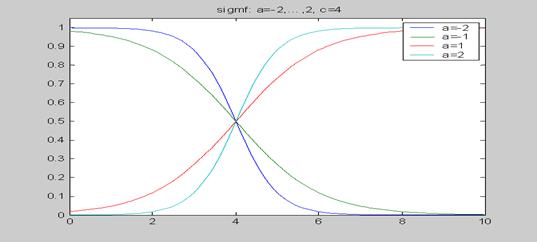
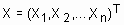 – объекты, подлежащие кластеризации, где n – количество объектов. Каждый объект
– объекты, подлежащие кластеризации, где n – количество объектов. Каждый объект 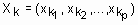 представляет собой точку в p-мерном пространстве признаков (
представляет собой точку в p-мерном пространстве признаков (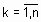 ). Необходимо найти центры кластеров, т.е. координаты центров скопления объектов, заданных множеством X.
). Необходимо найти центры кластеров, т.е. координаты центров скопления объектов, заданных множеством X.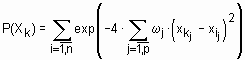 , где
, где 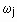 - вес j-й координаты. В случае, когда объект задан двумя признаками, графическое изображение распределения потенциала будет представлять собой поверхность, напоминающую горный рельеф. Отсюда и название - горный метод. В качестве центров кластеров выбирают координаты “горных” вершин. Для этого, центром первого кластера назначают объект с наибольшим потенциалом. Затем центр кластера а также близко расположенные к нему объекты исключают из дальнейшего рассмотрения, т.е. из “горного массива” вычленяют наивысшую “гору”. Значения потенциалов оставшихся объектов пересчитывают, и вновь в качестве центра кластера выбирают объект с максимальным значением потенциала. Итерационная процедура выбора центров кластеров продолжается до тех пор, пока не будут исключены все объекты.
- вес j-й координаты. В случае, когда объект задан двумя признаками, графическое изображение распределения потенциала будет представлять собой поверхность, напоминающую горный рельеф. Отсюда и название - горный метод. В качестве центров кластеров выбирают координаты “горных” вершин. Для этого, центром первого кластера назначают объект с наибольшим потенциалом. Затем центр кластера а также близко расположенные к нему объекты исключают из дальнейшего рассмотрения, т.е. из “горного массива” вычленяют наивысшую “гору”. Значения потенциалов оставшихся объектов пересчитывают, и вновь в качестве центра кластера выбирают объект с максимальным значением потенциала. Итерационная процедура выбора центров кластеров продолжается до тех пор, пока не будут исключены все объекты.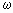 из формулы расчета потенциала связаны с radii следующим соотношением
из формулы расчета потенциала связаны с radii следующим соотношением 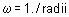 . Если аргумент radii задан скаляром, тогда все координаты считаются равноважными;
. Если аргумент radii задан скаляром, тогда все координаты считаются равноважными;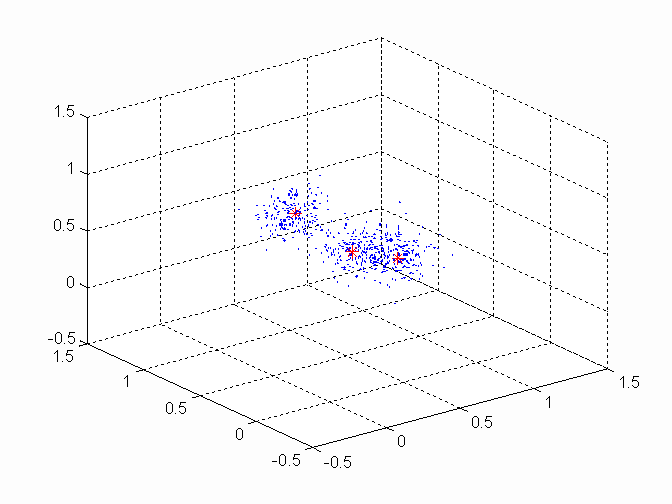
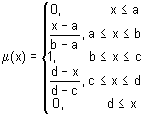 .
.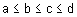 .
.
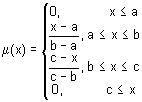 .
. .
.