Частотный диапазон и спектры
Акустический сигнал от каждого из первичных источников звука, используемых в системах вещания и связи, как правило, имеет непрерывно изменяющиеся форму и состав спектра. Спектры могут быть высоко – и низкочастотными, дискретными и сплошными. В первую очередь представляют интерес средний спектр для источников звука каждого типа, а для оценки искажений сигнала – спектр, усредненный за длительный интервал. Усредненный спектр может быть, как правило, сплошной и достаточно сглаженный по форме. Сплошные спектры характеризуются зависимостью спектральной плотности от частоты (эту зависимость называют энергетическим спектром). Спектральной плотностью называется интенсивность звука в полосе частот шириной, равной единице частоты. Для акустики эту полосу берут равной 1 Гц. Спектральная плотность Для удобства оценки введена логарифмическая мера плотности спектра аналогично уровню интенсивности. Эту меру называют уровнем спектральной плотности или спектральным уровнем. Спектральный уровень
Очень часто для характеристики спектра вместо спектральной плотности используют интенсивности и уровни интенсивности, измеренные в октавной, полуоктавной или третьоктавной полосе частот. Нетрудно установить связь между спектральным уровнем и уровнем в октавной (полуоктавной или третьоктавной) полосе. Спектральный уровень
а уровень в октавной полосе
где Вычитая второе из первого, находим
При известном спектре сигнала можно определить его суммарную интенсивность. Так, если спектр задан в уровнях интенсивности для третьоктавных полос, то достаточно перевести эти уровни (в каждой из полос) в интенсивности
Если спектр задан в спектральных уровнях, то, исходя из их определения, для всего спектра точный суммарный уровень
где
|

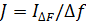 , где
, где 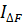 – интенсивность, измеренная в узкой полосе частот
– интенсивность, измеренная в узкой полосе частот  с помощью узкополосных фильтров.
с помощью узкополосных фильтров.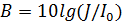 , где
, где 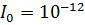
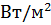 – интенсивность, соответствующая нулевому уровню, как и для оценки уровня интенсивности.
– интенсивность, соответствующая нулевому уровню, как и для оценки уровня интенсивности. , (1.21)
, (1.21)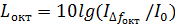 , (1.22)
, (1.22)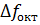 – ширина соответствующей октавной полосы.
– ширина соответствующей октавной полосы.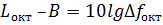 . (1.23)
. (1.23)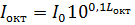 и затем просуммировать все интенсивности. Сумма всех
и затем просуммировать все интенсивности. Сумма всех 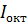 дает суммарную интенсивность
дает суммарную интенсивность 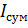 для всего спектра. Суммарный уровень
для всего спектра. Суммарный уровень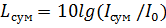 . (1.24)
. (1.24)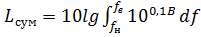 , (1.25)
, (1.25)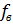 и
и 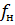 – верхняя, и нижняя границы частотного диапазона. Приближенно суммарный уровень можно найти делением частотного диапазона на
– верхняя, и нижняя границы частотного диапазона. Приближенно суммарный уровень можно найти делением частотного диапазона на 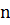 полосок шириною
полосок шириною 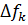 , в пределах которых спектральный уровень
, в пределах которых спектральный уровень 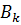 примерно постоянен. Суммарный уровень
примерно постоянен. Суммарный уровень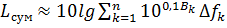 . (1.26)
. (1.26)


