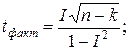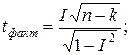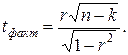Парная корреляция. Теоретическая часть
При парной корреляции устанавливают зависимость между двумя признаками, один из которых является факторным, другой - результативным. Связь между ними может иметь различный характер. Поэтому важно правильно установить форму связи между признаками и в соответствии с этим подобрать математическое уравнение, выражающее эту связь. Вопрос о форме связи можно решить несколькими способами: на основе логического анализа, по данным статистической группировки или графическим способом. При парной корреляции предпочтителен последний способ, так как он позволяет выявить не только характер связи, но дает представление о степени связи. После того, как определен вид уравнения связи, необходимо найти числовые значения его параметров. При вычислении параметров применяют различные методы: метод наименьших квадратов, метод средних, метод наименьшего предельного уклонения и др. Наиболее распространенным является метод наименьших квадратов. При его использовании находят такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических данных от расчетных является минимальной:
где y – фактическое значение результативного признака;
Для этого решают систему нормальных уравнений, которые строятся следующим образом. Исходное уравнение перемножают сначала на коэффициент при первом неизвестном и полученные данные суммируют. Затем исходное уравнение перемножают на коэффициент при втором неизвестном, полученные данные также суммируют и т. д. Рассмотрим, как получается система нормальных уравнений для уравнения линейной регрессии В данном уравнении коэффициент при первом неизвестном а 0 равен 1. Следовательно, исходное уравнение после перемножения сохраняет прежний вид:
а после суммирования
Коэффициент при втором неизвестном a 1 равен x. Умножая на него все члены исходного уравнения, получим:
а после суммирования
Значения
Правила получения системы нормальных уравнений распространяются на все виды уравнений регрессии. После того, как определены параметры уравнения регрессии, необходимо его оценить, то есть проверить, насколько оно соответствует изучаемой совокупности и как тесно связан результативный признак с фактором, обусловливающим его уровень. Для этого сравнивают вариацию значений результативного признака, рассчитанных по уравнению регрессии, то есть зависящих от факторного признака, с вариацией фактических (исходных) значений результативного признака. Чем ближе первая вариация будет ко второй, тем в большей степени уравнение регрессии отражает связь между признаками, тем теснее они связаны. Показатель, характеризующий отношение вариаций расчетных и исходных значений результативного признака, называют индексом корреляции. Его рассчитывают по формуле:
где I – индекс корреляции;
n – численность совокупности. Индекс корреляции изменяется в пределах от 0 до 1. Он показывает, что чем ближе его значение к 1, тем сильнее связь между признаками, и тем лучше уравнение регрессии описывает взаимосвязь между признаками. При индексе корреляции равном 1 взаимосвязь между признаками является функциональной. Если же индекс корреляции равен 0, то связь между признаками отсутствует. Поскольку факторная дисперсия показывает вариацию результативного признака, зависящую от факторного признака, то можно рассчитать остаточную дисперсию, показывающую вариацию других неучтенных факторов. Она равна разнице между общей и факторной дисперсиями:
где Остаточная дисперсия показывает вариацию фактических значений результативного признака относительно расчетных значений, то есть колеблемость фактических значений относительно линии регрессии. Чем меньше будет эта колеблемость, тем в большей степени уравнение регрессии отражает связь между признаками. Формула индекса корреляции, рассчитанного на основе остаточной и общей дисперсий, имеет вид:
Для линейной регрессии индекс корреляции называют коэффициентом корреляции. Формула его при парной корреляции после преобразования имеет вид:
где r – коэффициент корреляции;
В отличие от индекса корреляции коэффициент корреляции показывает не только тесноту связи, но и ее направление, поскольку меняется в пределах от −1 до +1. Если коэффициент корреляции положительный, то связь между признаками прямая (прямо пропорциональная), если отрицательный, то связь обратная (обратно пропорциональная). Квадраты индекса корреляции и коэффициента корреляции называют соответственно индексом детерминации (I 2) и коэффициентом детерминации (r 2). Индекс детерминации и коэффициент детерминации показывают, какая доля общей вариации результативного признака определяется изучаемым фактором. Так как надежность изучения связей в значительной степени зависит от количества сопоставляемых данных, необходимо измерять существенность полученного уравнения регрессии и индекса (коэффициента) корреляции. Показатели корреляции, исчисленные для ограниченной по объему совокупности, могут быть искажены действием случайных факторов. Существенность индекса (коэффициента) корреляции, а, следовательно, всего уравнения регрессии, может быть оценена с помощью дисперсионного анализа (F -критерия Фишера). При этом сравнивают факторную и остаточную дисперсии с учетом числа степеней свободы вариации. F -критерий в данном случае рассчитывают по формуле:
где
n – численность выборочной совокупности; k – число параметров в уравнении регрессии. Значение F -критерия можно получить также, используя значения индекса или коэффициента корреляции:
Полученное значение F-критерия сравнивают с табличным значением. При этом для факторной дисперсии число степеней свободы вариации составляет Для оценки значимости индекса (коэффициента) корреляции и уравнения регрессии также используют t -критерий Стьюдента, который для больших выборок рассчитывают по формулам:
Для малых выборок формулы имеют вид:
Также, как при дисперсионном анализе, фактическое значение t -критерия сравнивают с табличным с учетом числа степеней свободы вариации n = n - k. Если фактическое значение t -критерия больше табличного, то связь достоверна, если меньше, то связь несущественна.
|

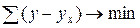 ,
, - расчетное значение результативного признака.
- расчетное значение результативного признака. .
.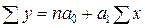 .
. ,
, .
. ,
, 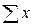 ,
,  и
и 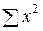 рассчитывают по данным наблюдения, а неизвестные параметры a 0 и a 1-путем решения системы уравнений:
рассчитывают по данным наблюдения, а неизвестные параметры a 0 и a 1-путем решения системы уравнений: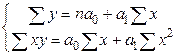
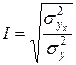 ,
, - общая дисперсия результативного признака (средний квадрат отклонений фактических значений у от средней
- общая дисперсия результативного признака (средний квадрат отклонений фактических значений у от средней  );
);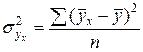 - факторная дисперсия результативного признака, рассчитанного по уравнению регрессии (средний квадрат отклонений расчетных значений
- факторная дисперсия результативного признака, рассчитанного по уравнению регрессии (средний квадрат отклонений расчетных значений  ,
, - остаточная дисперсия.
- остаточная дисперсия.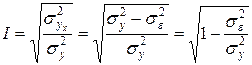
 .
. ,
,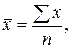
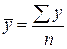 - средние значения факторного и результативного признаков;
- средние значения факторного и результативного признаков;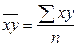 - среднее значение произведений факторного и результативного признаков;
- среднее значение произведений факторного и результативного признаков;
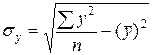 - средние квадратические отклонения факторного и результативного признаков.
- средние квадратические отклонения факторного и результативного признаков.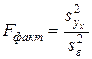 ,
, - выборочная факторная дисперсия;
- выборочная факторная дисперсия;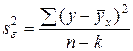 - выборочная остаточная дисперсия;
- выборочная остаточная дисперсия;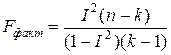 ;
;  .
.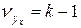 , а для остаточной дисперсии
, а для остаточной дисперсии  Если фактическое значение F -критерия больше табличного, следовательно, связь между признаками достоверна и уравнение регрессии в полной мере отражает эту связь. Если фактическое значение F -критерия меньше табличного, то можно сделать вывод, что связь между признаками носит случайный характер.
Если фактическое значение F -критерия больше табличного, следовательно, связь между признаками достоверна и уравнение регрессии в полной мере отражает эту связь. Если фактическое значение F -критерия меньше табличного, то можно сделать вывод, что связь между признаками носит случайный характер.