Графическое представление данных

 

Для графического представления интервальных рядов распределения настрига шерсти были построены гистограмма, полигон и кумулята распределения (рис.1, рис.2, рис.3).

 

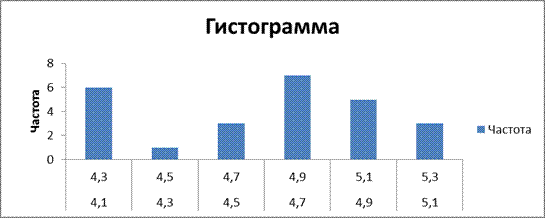
Рисунок 1. Гистограмма распределения величины настрига шерсти

 

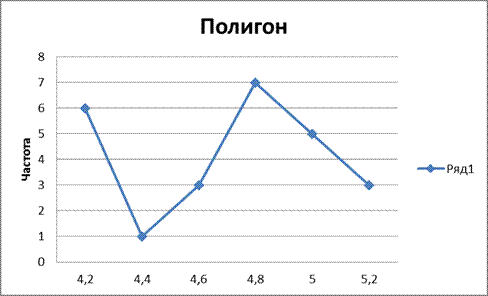
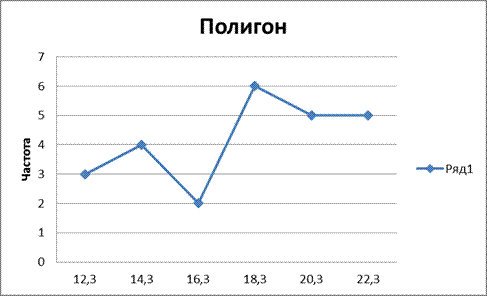
Рисунок 2. Полигон распределения величины настрига шерсти

 

Данные гистограммы и полигона распределения показывают характерную для многих признаков форму распределения: часто встречаютя значения средних интервалов признака, реже – крайние (малые и большие). Форма это распределения близка к форме нормального распределения, которое образуется если на варьирующую переменную влияет большое число факторов, но ни один из них не имеет преобладающего значения. Самую большую группу сосатвляют овцы со средним показателем величины настрица шерсти, а самую малую – с низким. Выделяется также самый маленький показатель величины настрига шерсти (4,2), поскольку его частота составляет 6, тогда как наимобльшая частота показателя – 7.

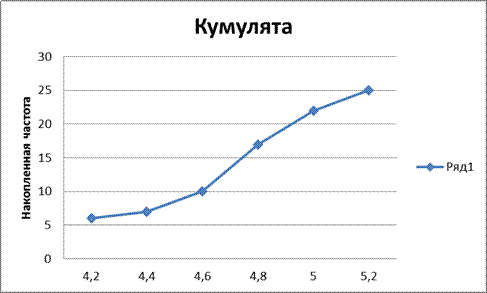
Рисунок 3. Кумулята распределения величины настрига шерсти

 

Для графического представления интервальных рядов распределения длины волоса шерсти были построены гистограмма, полигон и кумулята распределения (рис. 4, рис.5, рис.6).

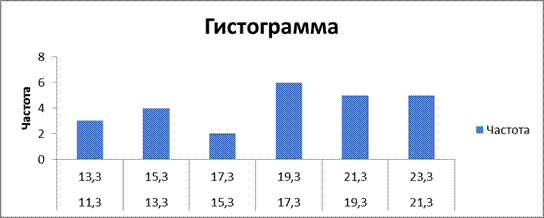
Рисунок 4. Гистограмма распределения длины волоса шерсти

Рисунок 5. Полигон распределения длины волоса шерсти

 

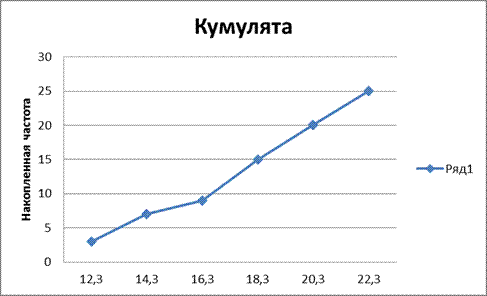
Рисунок 6. Кумулята распределения длины волоса шерсти

 

Данные показывают, что распределение длины волоса шерсти не является нормальным. Больше всего частота срединного интервала, однако наиболее высокие показатели распределения длины волоса шерсти имеют частоту, лишь на одну единицу отличающуюся от наибольшей. Наименьшая часто встречающимся показателем является показатель 16,3, который не является наименьшим.