Показатели вариации и распределения. Теоретическая часть
Для измерения вариации применяют различные показатели, из которых основными являются размах вариации (лимит), среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Размах вариации определяется как разница между наибольшим и наименьшим значениями признака:
где R -размах вариации; x min, xmax- минимальное и максимальное значение признака. Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных отклонений отдельных вариант от средней арифметической: простое взвешенное где L - среднее линейное отклонение;
х -варианты; n - число вариант; f - частоты. Дисперсию рассчитывают как среднюю арифметическую квадратов отклонений вариант от средней арифметической: простая взвешенная где Среднее квадратическое отклонение равно корню квадратному из дисперсии: простое взвешенное где Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической величине:
где Общий объем вариации для совокупности определяют как сумму квадратов отклонений индивидуальных значений признака от общей средней:
где wо - общая вариация;
xij -варианты; k -число групп; ni - численность групп; N - численность совокупности. Групповая вариация равна сумме квадратов отклонений групповых средних от общей средней:
где wгр - групповая вариация;
При равной численности групп формула принимает вид:
Остаточную вариацию определяют как сумму квадратов отклонений индивидуальных значений признака от средней по группам:
где wост - остаточная вариация. При равной численности групп формула имеет вид:
Групповая и остаточная вариации в сумме равны общей вариации:
Данное равенство называется правилом разложения (сложения) вариации. Отсюда, зная две величины, можно определить третью. Коэффициент асимметрии для выборки рассчитывается по формуле:
где As – коэффициент асимметрии;
n – число вариант. Показатель эксцесса для выборки рассчитывается по формуле:
где
|

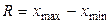 ,
, ;
; ,
,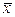 - средняя арифметическая;
- средняя арифметическая;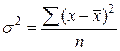 ;
; ,
, - дисперсия.
- дисперсия.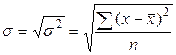 ;
;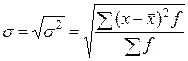 ,
, - среднее квадратическое отклонение
- среднее квадратическое отклонение ,
,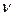 -коэффициент вариации.
-коэффициент вариации.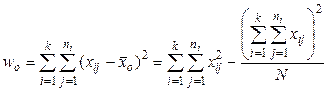 ,
,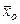 - общая средняя арифметическая;
- общая средняя арифметическая; ,
, - групповые средние арифметические.
- групповые средние арифметические. .
. ,
, .
. .
.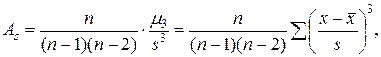
 – момент третьего порядка;
– момент третьего порядка; – выборочное среднее квадратическое отклонение;
– выборочное среднее квадратическое отклонение;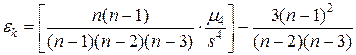 или
или  ,
,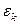 – эксцесс;
– эксцесс;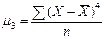 – момент четвертого порядка.
– момент четвертого порядка.


