Расчет средних величин. Теоретическая часть
Средняя арифметическая является наиболее распространенной среди средних величин. Ее применяют в тех случаях, когда даны отдельные объекты с индивидуальными значениями признаков, выраженными абсолютными показателями. Среднюю арифметическую определяют как отношение суммы индивидуальных значений признаков к их количеству. Различают среднюю арифметическую простую и взвешенную. Среднюю арифметическую простую применяют в случае, если индивидуальные значения признака в совокупности встречаются по одному разу, а взвешенную - если индивидуальные значения признака представлены несколькими объектами. Среднюю арифметическую простую определяют по формуле:
где х -варианты; n -число вариант. Формула средней арифметической взвешенной имеет вид:
где f -частота вариант. Средняя гармоническая является обратной величиной средней арифметической, рассчитанной из обратных значений признака. В качестве частот в этом случае используются не единицы совокупности, а произведения этих единиц на значения признака. Среднюю гармоническую применяют в тех случаях, когда известны индивидуальные значения и объемы признака, а частоты неизвестны. Формула средней гармонической имеет вид:
где х -варианты; Средняя геометрическая — это средняя, в которой общий объем явления представляет произведение индивидуальных значений признака. Такую среднюю применяют в основном для расчета среднего темпа изменения какого-либо показателя за определенный промежуток времени. Формула расчета средней геометрической имеет вид:
где х -варианты; n -число вариант; П — произведение. Среднюю квадратическую используют для признаков, выраженных линейными мерами площади. Например, для определения среднего диаметра корзинок подсолнечника, величины листьев, размера колоний микроорганизмов и др. Также как и средняя арифметическая, средняя квадратическая бывает простая и взвешенная. Среднюю квадратическую простую определяют по формуле:
где х -варианты; n -число вариант. Формула средней квадратической взвешенной имеет вид:
где f -частота вариант. Мода - это величина, которая встречается в совокупности наиболее часто, то есть признак с наибольшей частотой. Этот показатель используется в тех случаях, когда требуется охарактеризовать наиболее часто встречающуюся величину признака (наиболее распространенный размер животноводческих ферм на сельскохозяйственных предприятиях, преобладающие цены на сельскохозяйственную продукцию и т. п.). Медианой называется величина, делящая численность упорядоченного вариационного ряда (расположенного в порядке возрастания или убывания признака) на две равные части. Медиана характеризует количественную границу значений изменяющегося признака, которыми обладает половина единиц совокупности. Например, если медианное значение удоя коровы составляет 4735 кг, то это означает, что половина коров имеет удой молока ниже 4735 кг и половина коров выше. В дискретном вариационном ряду модой является признак с наибольшей частотой. Медианой является признак с номером, который находят путем деления суммы частот упорядоченного вариационного ряда на два и добавления 0,5. В интервальном вариационном ряду моду находят по формуле:
где Мо - мода; хМо -нижняя граница модального интервала; hМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным. Модальным интервалом является интервал с наибольшей частотой. Формула расчета медианы в интервальном вариационном ряду:
где Ме - медиана; хМе - нижняя граница медианного интервала; hМе - величина медианного интервала;
sМе−1 - сумма частот, накопленных в интервалах, предшествующих медианному; fМе - частота медианного интервала. Медианным интервалом является интервал, накопленная частота которого равна или превышает половину суммы частот.
|

 ,
,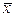 -средняя;
-средняя;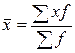 ,
,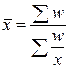 ,
, ,
, ,
,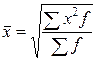 ,
,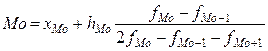 ,
, ,
,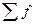 - сумма частот;
- сумма частот;


