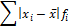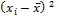Рассчитать абсолютные и относительные показатели вариации. Сделать выводы.
Вариант 1 Задание №1 Распределение промышленных предприятий региона по показателю затрат на 1 тыс. руб. продукции в сентябре следующее
Определить: 1. Средний размер затрат на 1 тыс. руб. продукции по предприятиям региона; 2. Средний объем продукции на одно предприятие.
Задание № 2 Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов:
Рассчитать абсолютные и относительные показатели вариации. Сделать выводы.
Алгоритм решения:
1) Размах вариации: R=Xmax –Xmin 2) Среднее линейное отклонение: 3) Дисперсия: 4) Среднее квадратическое отклонение:
1) Коэффициент осцилляции: 2) Относительное линейное отклонение (Линейный коэффициент вариации): 3) Коэффициент вариации: Для решения рекомендуется создать следующую вспомогательную таблицу:
Выводы (пример выводов ): Размах вариации показывает расстояние между двумя крайними точками рассматриваемого явления: в данном случае число слов в телеграмме. Таким образом видим, что разница между телеграммами с наибольшим и наименьшим количеством слов составила ____ слов. Среднее линейное отклонение даёт обобщенную характеристику степени колебания признака в рассматриваемой совокупности. В рассматриваемом примере видим, что разница между значениями совокупности составляет в среднем ____ слова Среднее квадратическое отклонение показывает средний квадрат отклонения каждой точки исследуемой совокупности от средней величины. В нашем примере это ______слова Коэффициент осцилляции показывает относительный размах вариации к средней величине исследуемого признака Линейный коэффициент вариации показывает относительное отклонение исследуемого признака по модулю от средней величины. Коэффициент вариации как относительное квадратическое отклонение оценивает степень интенсивности вариации рассматриваемого признака совокупности.
|

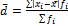
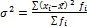
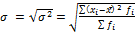
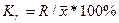

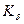 =
= 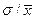 *100%
*100%