Представление гармонических колебаний векторами
Для непосредственного сложения синусоидальных функций необходимо производить достаточно громоздкие операции. Существенное упрощение достигается, если синусоидальную функцию изобразить в виде вращающегося вектора. Векторное изображение синусоиды строится следующим образом (см. рис. 3.2).
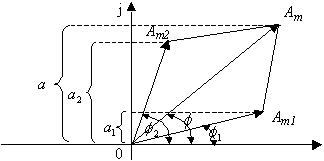
Рис. 3.2. На плоскости из начала координат под углом Построим векторное изображение суммы двух функций (рис. 3.3): Очевидно, что вместо сложения синусоид удобно геометрически складывать их векторные изображения. Таким образом, получили простейшую векторную диаграмму.
Рис. 3.3. Векторная диаграмма представляет собой совокупность векторов, изображающих синусоидальные функции одинаковой частоты, построенных с соблюдением масштаба и правильной ориентации их друг относительно друга по фазе. Условились: вместо амплитуд на векторных диаграммах откладывать действующее значение функции.
|
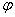, равному начальной фазе синусоиды, проводится прямая и на ней откладывается в масштабе отрезок, равный амплитуде колебания. Угол 
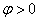; и по часовой стрелке, если 
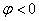. Если угол 
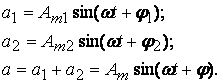(3.5)
