Последовательное соединение элементов R, L, C
Рис. 3.7. По цепи протекает ток На основании второго закона Кирхгофа uR+uL+uC = u, или Подставляя значения тока i, получим Так как Величины Для определения Получим
Выводы: - если по участку цепи с последовательным соединением RLC - элементов протекает синусоидальный ток, то напряжение на этом участке также будет синусоидальным, но фаза напряжения будет отличаться от фазы тока на величину - если - ток совпадает по фазе с напряжением при
а)
Рис. 3.8. Вопросы для самоконтроля к лекции 3 1. Какие напряжения (токи) называют гармоническими? 2. Как связаны частота f и период Т гармонических сигналов? 3. Что называют фазой и начальной фазой гармонического напряжения (тока)? Нарисуйте кривые гармонических сигналов, сдвинутые относительно друг друга по фазе. Объясните, какие кривые являются опережающими и какие отстающими. 4. Как строят векторные диаграммы гармонических напряжений (токов)? 5. Для каких значений гармонических напряжений и токов выполняются законы Ома? 6. Чем объясняется наличие фазового сдвига между напряжением и током в индуктивности и емкости? 7. Объясните изменение мгновенной мощности на элементах цепи. 8. Разберите решения задач 2.1-2.3, 2.6, 2.10 из [4]. 9. Решите задачи 2.5, 2.8 из [4]. Литература: [1] с.98-114; [2] с.37-46; [3] с. 28-46; [5] с. 151-157.
|



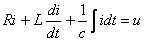 (3.14)
(3.14) (3.15)
(3.15)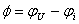 , то ji + f = jU и u = Um sin(wt + yi + j).
, то ji + f = jU и u = Um sin(wt + yi + j). называется реактивным сопротивлением цепи. Если
называется реактивным сопротивлением цепи. Если 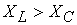 , то реактивное сопротивление X>0 - имеет индуктивный характер; если
, то реактивное сопротивление X>0 - имеет индуктивный характер; если  то X<0 – емкостной характер.
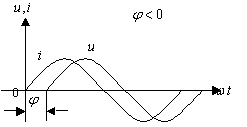
то X<0 – емкостной характер.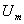 и
и 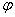 воспользуемся тригонометрическими соотношениями:
воспользуемся тригонометрическими соотношениями:

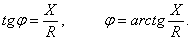
 называется полным сопротивлением цепи.
называется полным сопротивлением цепи.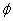 ;
;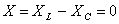 (рис.3.8, в). Такой режим работы электрической цепи называется резонансным, напряжение на индуктивности и емкости компенсируют друг друга, и в цепи имеет место резонанс напряжений.
(рис.3.8, в). Такой режим работы электрической цепи называется резонансным, напряжение на индуктивности и емкости компенсируют друг друга, и в цепи имеет место резонанс напряжений.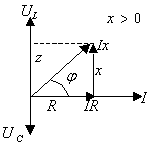
 Временные и векторные диаграммы цепи RLC для трех случаев приведены на рис. 3.8.
Временные и векторные диаграммы цепи RLC для трех случаев приведены на рис. 3.8.
 б)
б)
 в)
в)


