Изображение производной и интеграла от синусоидальной функции
Пусть Тогда Операция дифференцирования синусоидальной функции соответствует умножению на Пример: С производной мы встречаемся при определении напряжения на индуктивности При откуда имеем При этом получаем комплексное сопротивление индуктивности При т.е. соответствует делению на jw ее комплексного изображения. Пример: С интегралом мы встречаемся при определении напряжения на емкости Для вращающихся векторов получим откуда имеем, Пример: Рассмотрим цепь RLC (рис.4.2.).
Рис. 4.2. У равнение цепи для мгновенных значении напряжений имеет вид: При
|
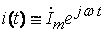, где 
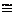знак соответствия,
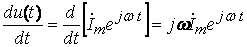, т.е.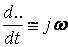
ее комплексного изображения.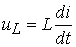
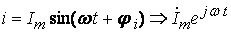- для вращающихся векторов получим:
,
.
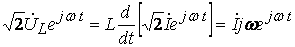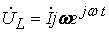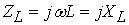, как чисто мнимое число.
, (4.7)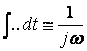
- операция интегрирования синусоидальной функции
.
,
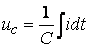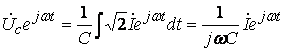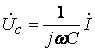
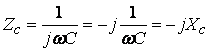- комплексное cопротивление емкости (4.8)
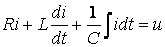
для комплексных зображений получим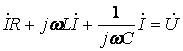
.
