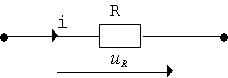
Активное сопротивление
По закону Ома имеем:
Временная и векторная диаграммы представлены на рис. 3.4.
Рис. 3.4. Углом сдвига фаз межу током и напряжением Выводы: - напряжение на участке с активным сопротивлением при синусоидальном токе будет также синусоидальным, при этом напряжение и ток совпадают по фазе, амплитуда напряжения равна - закон Ома для участка с активным сопротивлением одинаково справедлив и для мгновенных значений, и для амплитуд, и для действующих значений. Мгновенная мощность PR = uRi содержит две составляющие: постоянную и переменную, которая изменяется по закону косинуса с частотой Среднее за период значение мгновенной мощности (называется активной мощностью) равно:
Напряжение на индуктивности определяется по закону электромагнитной индукции Обозначим Выводы: – если ток на индуктивности изменяется по синусоидальному закону, то и напряжение также изменяется синусоидальному закону, однако начальные фазы этих синусоид не совпадают – они сдвинуты на – если величину
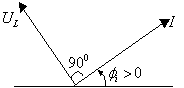
а) временные диаграммы б)векторная диаграмма Рис. 3.5. Мгновенная мощность Средняя (активная) мощность на участке с индуктивностью равна нулю, но энергия на этом участке пульсирует. Когда ток возрастает от нуля до максимума по абсолютной величине, мощность
|

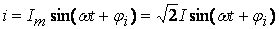
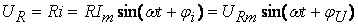

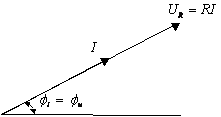
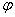 называется разность начальных фаз напряжения и тока
называется разность начальных фаз напряжения и тока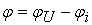 .
.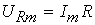 ;
;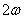
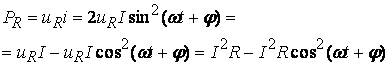 (3.8)
(3.8)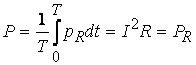 (3.9)
(3.9) 2. Индуктивность
2. Индуктивность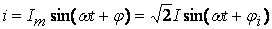
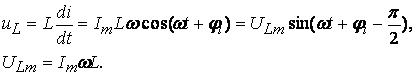 (3.10)
(3.10)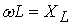 , тогда ULm = ImXL или uL = IXL
, тогда ULm = ImXL или uL = IXL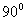 (рис. 3.5), кривая напряжения опережает кривую тока на
(рис. 3.5), кривая напряжения опережает кривую тока на 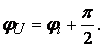 ;
;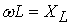 называть индуктивным сопротивлением, то амплитуда напряжения на индуктивности будет равна произведению амплитуды тока и индуктивного сопротивления. Следовательно, получается формула, аналогичная закону Ома. Точно также связаны действующие значения напряжения и тока. Мгновенные значения закону Ома не подчиняются.
называть индуктивным сопротивлением, то амплитуда напряжения на индуктивности будет равна произведению амплитуды тока и индуктивного сопротивления. Следовательно, получается формула, аналогичная закону Ома. Точно также связаны действующие значения напряжения и тока. Мгновенные значения закону Ома не подчиняются.
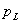 будет равна
будет равна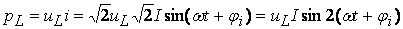 .
.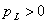 (положительна), энергия поступает от источника в индуктивность и там накапливается в виде энергии магнитного поля Wm = Li2/2. Когда ток уменьшается от max до 0, энергия переходит из магнитного поля обратно в источник, мощность
(положительна), энергия поступает от источника в индуктивность и там накапливается в виде энергии магнитного поля Wm = Li2/2. Когда ток уменьшается от max до 0, энергия переходит из магнитного поля обратно в источник, мощность 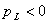 .
.


