Символическое изображение синусоидальных функций комплексными величинами
Любую гармоническую функцию a)
Рис. 4.1. Существуют три формы записи комплексного числа 1. 2. 3. часть). Переход от одной формы записи к другой можно осуществить с помощью формул: Необходимо запомнить: Комплексной амплитудой В значением - комплексным током.
Составим новое комплексное число
которое называется вращающимся вектором тока. Разложим Следовательно, синусоидальный ток является мнимой частью вращающегося вектора, т.е. где j - знак мнимой части. Часто величины i, u, называют оригиналами, а 1) 2) 3)
|

 можно изобразить в виде вектора (рис. 4.1, а), а каждому вектору можно поставить в соответствие комплексное число (рис. 4.1, б).
можно изобразить в виде вектора (рис. 4.1, а), а каждому вектору можно поставить в соответствие комплексное число (рис. 4.1, б).
 - показательная (А - модуль комплексного числа, j - его аргумент);
- показательная (А - модуль комплексного числа, j - его аргумент); - тригонометрическая;
- тригонометрическая; - алгебраическая (а - вещественная часть, б - мнимая
- алгебраическая (а - вещественная часть, б - мнимая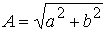 ;
;  ; (4.1)
; (4.1)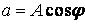 ;
;  .
. ;
;  ;
;  ;
;  . (4.2)
. (4.2) называется комплексная величина, модуль которой равен амплитуде синусоидального тока, а аргумент - начальной фазе.
называется комплексная величина, модуль которой равен амплитуде синусоидального тока, а аргумент - начальной фазе. раз меньшую величину называют комплексным действующим
раз меньшую величину называют комплексным действующим Аналогично
Аналогично - комплексная амплитуда напряжения;
- комплексная амплитуда напряжения; - комплексное напряжение.
- комплексное напряжение. (4.3)
(4.3)
 по формуле Эйлера:
по формуле Эйлера: (4.5)
(4.5) ,
, – их комплексными изображениями. Примеры:
– их комплексными изображениями. Примеры: ;
; ;
; .
.


